De straal van de aarde vanuit een ligstoel
Pythagorasredacteur Jan Guichelaar zat vorig jaar op het achterdek van het containerschip The Independent Voyager, op weg van Antwerpen naar Amerika. Hij bedacht daar een methode om – al schattend – de straal van de aarde te berekenen.
Twee manieren om de straal van de aarde te meten 13 zijn al eens in dit blad beschreven, zij het lang geleden. In nummer 5 van de vierde jaargang (beschikbaar op http://www.pyth.eu) stond het artikel ‘Hoe groot is de aarde?’, dat in 2011 ook werd opgenomen in het jubileumboek De Pythagoras Code. In dat artikel staan methoden van de Griek Eratosthenes (276-194 voor Chr.) en van de Nederlandse astronoom Jacobus Kapteyn (1851-1922).
Eratosthenes ontdekte dat de zon ’s middags om 12 uur precies boven Syene stond en tot op de bodem van een diepe waterput scheen. Hij wist ook dat in Alexandrië, op een afstand van 5.000 stadiën ten noorden van Syene, de zon een hoek van ruim $7^\circ$ maakte met de verticaal. Die hoek is ongeveer 1/50 deel van de cirkelomtrek. En daaruit concludeerde Eratosthenes dat de omtrek van de aarde ongeveer $50 \times 5000 = 250.000$ stadiën was. Nu weten we niet precies hoeveel een stadie was, maar iets in de buurt van 200 meter lijkt redelijk. Dat levert dan 50.000 kilometer op voor de omtrek van de aarde. Geen slechte schatting voor die tijd.
Kapteyn bedacht een creatieve andere manier. Hij liet twee mensen, waarbij de één een stuk boven de ander staat, beiden ja roepen als de zon precies onder gaat. Degene die het hoogste staat, zal een aantal seconden later ja roepen dan degene die beneden staat. Uit het tijdsverschil $t$ en het hoogteverschil $h$ kan de straal van de aarde berekend worden. Ik geef hier alleen de formule waar je de straal van de aarde $r$ uit kunt berekenen (je herkent de 24 uur waarin de aarde ronddraait om zijn as):
$$\left(\frac{t\times 2\pi r}{24\times 60 \times 60}\right)^2=2rh.$$
De afleiding van deze formule vind je in het genoemde artikel uit Pythagoras 4-5.
Op een dekstoel
Toen ik vorig jaar op het achterdek van het containerschip The Independent Voyager zat, op een spiegelgladde zee, op weg van Antwerpen in Belgi. naar Amerika, kwam ik plotseling op een andere methode om de straal van de aarde te berekenen.
Ik zat op een dekstoel aan het begin van een 20 meter lange railing die horizontaal dwars over het schip liep. Voor de schatting van 20 meter hoefde ik mijn stoel niet uit, want ik wist dat het gehele schip 30 meter breed was en vanuit mijn stoel kon ik goed schatten dat de afstand van het begin van de railing tot de stuurboordkant 5 meter was. Met diezelfde 5 meter aan de bakboordkant was mijn schatting van de lengte van de railing van 20 meter wel reëel.
Toen ik met mijn oog (ik hoefde niet eens op te staan) precies boven langs de railing keek, keek ik naar een punt boven de horizon. Door nu mijn hoofd met mijn oog een paar centimeter naar boven te verplaatsen en precies over het einde van de railing, dus een tikkeltje naar beneden, te kijken, zag ik precies de horizon. Na wat prutsen met mijn vinger naast mijn hoofd kon ik een schatting maken van het stukje dat ik mijn hoofd moest optillen om precies de horizon te zien. Mijn schatting was 4,5 centimeter.
Nu had ik twee gegevens: 20 meter en 4,5 centimeter. Maar ik kon nog een derde gegeven goed schatten: de hoogte van mijn oog boven het zeeoppervlak. Ik zat op het derde dek boven het hoofddek. De afstand tussen twee dekken was 3 meter. De afstand tussen het hoofddek en het zeeoppervlak had ik al eens geschat: zo’n 6 meter. Mijn oog bevond zich op ongeveer 1 meter boven het derde dek. In totaal was mijn oog dus zo’n 16 meter boven het zeeoppervlak.
Wat kon ik met deze drie getallen – 20 meter, 4,5 centimeter en 16 meter – aanvangen? De ogen sluiten, lang nadenken in het zonnetje, het hoofdrekenen tot kunst verheffen, en ik kon de straal van de aarde bij benadering berekenen.
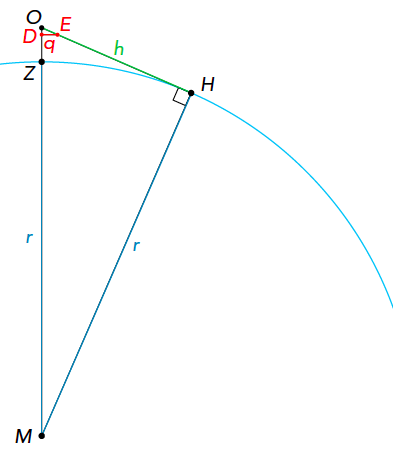
Verder: $z = OZ, p = OD, q = DE, h = OH, r = MH = MZ$.
De berekening
Kijk eerst eens naar de schets hierboven. De cirkel geeft het aardoppervlak aan. De railing is $DE$ en heeft lengte $q$. Mijn oog zit in punt $O$. De afstand tot het zeeoppervlak is $z = OZ$ en de afstand van mijn oog tot de railing is $p = OD$. De horizon zit bij $H$ en het middelpunt van de aarde is $M$. De straal van de aarde geven we aan met $r$. We zien dat de twee driehoeken $ODE$ en $OHM$ gelijkvormig zijn. Dat geeft de verhouding
$$\frac{q}{p} =\frac{r}{h}.\ \ \ \ \ \ (\star)$$
Nu heb ik weliswaar de verhouding van de onbekenden $r$ en $h$, maar hiermee zijn we er nog niet. We kunnen echter nog meer berekenen: in de grote
Pythagoras toepassen. Dat levert
$$(r + z)^2 = r^2 + h^2.$$
Uitwerken van de haakjes geeft
$$r^2 + 2rz + z^2 = r^2 + h^2.$$
Dat geeft
$$(2r + z)z = h^2.$$
Je ziet dat $r^2$ aan beide kanten tegen elkaar zijn weggestreept. Verder kun je vaststellen dat $z$ vele, vele malen kleiner is dan $r$. Ook al hebben we de straal van de aarde nog niet berekend, toch kunnen we dit wel stellen. Maar dan kunnen we in de laatste formule de $z$ tussen haakjes wel weglaten: ten opzichte van $2r$ is die te verwaarlozen. Dan hebben we
$$2rz = h^2. \ \ \ \ \ \ \ \ (\star \star)$$
Nu hebben we twee vergelijkingen voor onze twee onbekenden $r$ en $h$. Dus we kunnen niet alleen de straal van de aarde berekenen, maar ook de afstand tot de horizon.
Vermenigvuldig nu het linkerlid van ($\star \star$) met $\frac{q}{p}$ en het rechterlid van ($\star \star$) met $\frac{r}{h}$ (dat mag, want $\frac{q}{p}$ en $\frac{r}{h}$ zijn volgens ($\star$) aan elkaar gelijk):
$$2rz·\frac{q}{p} =h^2 ·\frac{r}{h}$$
ofwel
$$h =2z· \frac{q}{p}.$$
Nu vullen we onze geschatte getallen ($z = 16 m, q = 20 m, p = 0,045$ m) in:
$$h =2·16· \frac{20}{0,045}\approx 14.222m \approx 14,2 km.$$
Ten slotte berekenen we ons einddoel, de straal van de aarde, met behulp van ($\star$):
$$r =h\cdot \frac{q}{p} =14,2\cdot \frac{20}{0,045} \approx 6.311 km,$$ wat niet veel afwijkt van 6371 km, de werkelijke waarde.
Rechtvaardiging
Op mijn geschatte metingen zijn natuurlijk wel wat kritiekpunten te leveren. In de eerste plaats heb ik nog eens met grote stappen de lengte van de railing gemeten: 20 meter was niet gek. Vervolgens de hoogte boven het zeeoppervlak. De hoogte van elk dek van 3 meter heb ik niet nagemeten, noch bij de kapitein of stuurman nagevraagd. Dat had beter gekund. De schatting van de afstand van het hoofddek tot het wateroppervlak is ook aan enige twijfel onderhevig. Vervolgens de 4,5 centimeter. Dat is natuurlijk een meting die veel invloed heeft. 3 centimeter of 6 centimeter geeft al een enorm verschil. Een beetje geluk moet een mens hebben.
Dan is er de vraag of de railing wel echt goed horizontaal was. Is de dwarse horizontale railing wel echt waterpas? Daarover heb ik nog wel even nagedacht. Een schip met een paar duizend containers aan boord moet zeer precies horizontaal liggen in het water. De kans op kapseizen tijdens zwaar weer is anders te groot. Hoe wordt een containerschip perfect horizontaal gehouden? Ik heb mijn informatie van de kapitein (in het Engels aan boord: the master) en de eerste machinist (chief engineer). Van elke container wordt het gewicht en het zwaartepunt in de scheepscomputer ingevoerd. Daaruit wordt het zwaartepunt van de totale lading berekend. Indien dat zwaartepunt niet exact in het midden van het schip ligt, is er de mogelijkheid om dat te corrigeren door in een groot aantal vaten onder dek zeewater in te laten of naar buiten te pompen om het evenwicht perfect te maken (tot 20.000 ton). Op grond van deze gegevens is het aannemelijk dat de railing van 20 meter lang echt vrijwel horizontaal ligt.
Uiteindelijk gaat het niet om de exacte waarde, maar om de methode om de straal van de aarde te berekenen. Dat dat bij goede benadering kon was, zittend op het achterdek met enkel een blocnote en een pen, voor mij een leuke verrassing.