In 1964 (Pythagoras 4-5) werd het touw over de evenaar gelegd en moest de lezer het antwoord zelf vinden (of achterin het nummer kijken). Ook werd daar een (bijna equivalente) vraag gesteld: hoeveel touw moest er worden toe- gevoegd om het overal één meter hoog te krijgen.

In 1984 (Pythagoras 24-1) ging het touw ook over de evenaar. Daar werd het antwoord meteen voorgerekend, want er werd nog een, wat lastiger, probleem bekeken.

In 2004 (Pythagoras 44-2) ging het touw eindelijk over de polen. En in plaats van naar de hoogte van het touw vroegen we of er een muis onderdoor zou kunnen. En ook pakten we het lastigere probleem aan.

 

Opgave 1 Bereken zelf de antwoorden op de vragen: Hoe hoog komt het touw met één meter extra? Kan er inderdaad een muis onderdoor? Hoeveel touw moet erbij om het overal één meter hoog te krijgen? Je zult zien dat de plaatjes absoluut niet op schaal zijn en ook dat de straal van de aarde niet in de antwoorden voorkomt.

 

Opgave 2 Bereken of, beter, maak een schatting van het aantal mensen dat je nodig zult hebben om dat touw met de extra meter overal op te tillen. Heb je genoeg aan de bevolking van Nederland? Van Europa? De wereldbevolking?

De lastigere opgave

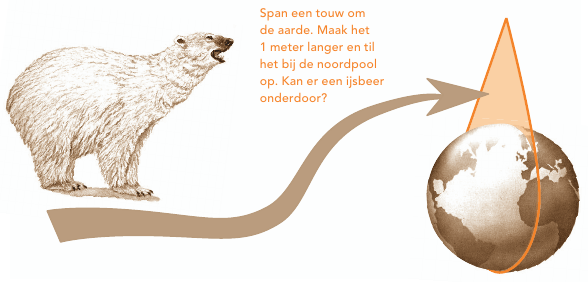
De lastigere opgave is wat er gebeurt als je in je eentje het verlengde touw optilt en strak trekt, zeg boven de noordpool. 

Hoeveel meter komen die vingers boven de Noordpool? De formulering in 2004 was iets beeldender: kan er een ijsbeer onder het touw door als we de aarde denkbeeldig aan een spijker boven de Noordpool op zouden hangen?

Maar wat is nu het antwoord?

In 1984 kwam men op $121{,}5$ m, en in 2004 vonden we $121{,}4$ m. Vrijwel hetzelfde dus, maar met een klein verschil. We gaan kijken waar dat verschil vandaan komt en ook naar de verschillen in aanpak in 1984 en 2004. In figuur 6 staat het plaatje uit 2004.

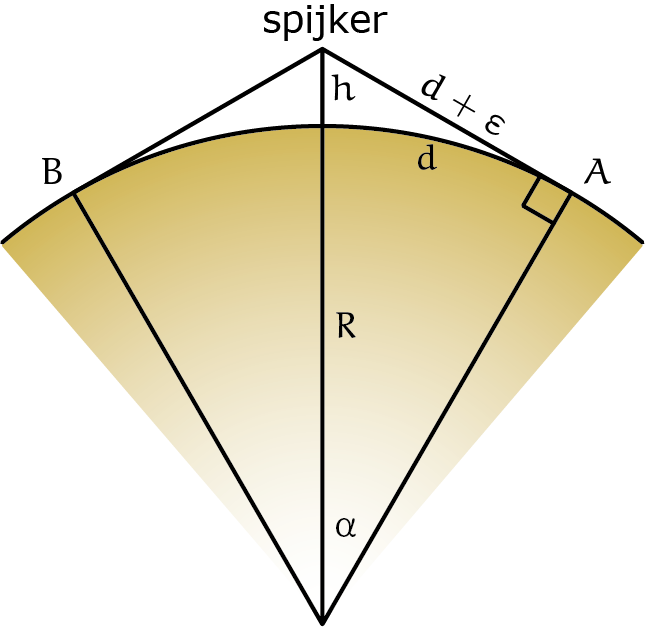
De belangrijke grootheden zijn de straal $R$ van de aarde en de lengte van het ingevoegde stuk touw, in het plaatje is $\varepsilon$ de helft daarvan omdat het hele stuk over de delen links en rechts van de spijker wordt verdeeld. Hiervan afgeleid zijn de lengte $d$ van de boog van $A$ (of $B$) naar het midden onder de spijker en de bijbehorende hoek $\alpha$. We werken in radialen, dus $d = \alpha R$ en $h$ is dan de lengte die we zoeken.

In 1984

In jaargang 24 werd alles met goniofuncties gedaan, en alleen voor $\varepsilon=\frac{1}{2}$. Uit de rechthoekige driehoek lezen we af dat

	$\cos(\alpha)$	$=$	$\frac{R}{R+h}$	en
	$\tan(\alpha)$	$=$	$\frac{d+\tfrac{1}{2}}{R}$

Omdat $d=\alpha R$ vinden we een vergelijking voor $\alpha$:

$\tan(\alpha)$

$=$

$\alpha+\frac{1}{2R}$

en daarnaast kunnen we via de cosinus $h$ in $R$ en $\alpha$ uitdrukken:

$$h=R\left(\frac{1}{\cos(\alpha)}\right)-1.$$

De straal $R$ is bekend, die werd gelijk genomen aan $6\,378\,000\ m$. De vergelijking voor $\alpha$ heeft geen makkelijke oplossing; je moet
een benadering maken. Om de berekeningen makkelijk te maken gebruikte men dat

$\tan(\alpha)-\alpha\approx\tfrac{1}{3}\alpha^3$

en

$\frac{1}{\cos(\alpha)}-1\approx\tfrac{1}{2}\alpha^2$.

Hiermee vind je dat

$$\alpha^3\approx\frac{3}{2R}$$

en dus

$$h\approx\frac{R}{2}\cdot\left(\frac{3}{2R}\right)^{\tfrac{2}{3}}=\frac{R^{\tfrac{1}{3}}3^{\tfrac{2}{3}}}{2^{\frac{5}{3}}}.$$

We zien dat het antwoord nu (ook) van $R$ afhangt. Invullen van de straal geeft nu dat $h \approx 121{,}5\ m$. We zullen straks zien waar die benaderingen vandaan komen en ook dat het verschil in uitkomsten niet aan de benaderingen ligt.

In 2004

In 2004 was het niet meer nodig de vergelijking te vereenvoudigen want de rekenmachientjes waren inmiddels wat beter geworden. Je kon bijvoorbeeld gewoon de vergelijking $\tan(\alpha)-\alpha=\frac{1}{2R}$ invoeren en naar $\alpha$ laten oplossen, na invullen van $R$ natuurlijk. We gebruikten niet de cosinus, maar de stelling van Pythagoras om $h$ in $\varepsilon$ en $R$ uit te drukken:

$$(R+h)^2=R+(d+\varepsilon)^2.$$

Omdat $R+h$ positief is kregen we

$$h=-R+\sqrt{R^2+(d+\varepsilon)^2}$$

en daar maakten we de indrukwekkende formule

$$h=R\left(\sqrt{1+\left(\frac{d+\varepsilon}{R}\right)^2}-1\right)$$

van. Nu moeten we nog $d$ bepalen. Dat leidt tot dezelfde vergelijking als in 1984, want $\frac{d+\varepsilon}{R}=\tan(\alpha)$ en $\frac{d}{R}=\alpha$, en dus

$$\tan(\alpha)=\alpha+\frac{\varepsilon}{R}.$$

Voor het oorspronkelijke probleem vulden we $R = 40\,000\,000/(2\pi)\ m$ en $\varepsilon=\tfrac{1}{2}$ in. Waar komt die $R$ vandaan? Uit de oorspronkelijke definitie van de (kilo)meter: de meridiaan door Parijs is tussen de Noordpool en de evenaar per definitie $10\,000\ km$ lang.

Daarom hebben we ons touw ook langs die meridiaan gelegd.

Met de grafische rekenmachine vinden we $\alpha = 0{,}006176$ (radialen) en dan $d = 39,320\ km$. Als we dat in de formule stoppen en die door de rekenmachine uit laten werken komt er $h \approx 121{,}4\ m$.

Het verschil in uitkomst ligt aan de waarden die voor $R$ gekozen werden. Als je in de formule uit 1984 de straal uit 2004 invult zul je $h \approx 121{,}4\ m$ vinden. En de straal uit 1984 levert met de methode van 2004 de waarde $h \approx 121{,}5\ m$.

In 2024: verklaring van de verschillen

Herinner dat we de halve lengte van het toegevoegde touw $\varepsilon$ hadden genoemd omdat we ook willen weten hoe $h$ van die hoeveelheid afhangt.

Net als in 1984 gebruikten we in 2004 dat $\tan(\alpha)-\alpha\approx\tfrac{1}{3}\alpha^3$ voor heel kleine waarden van $\alpha$. Dat hadden we een nummer eerder afgeleid (Pythagoras 44-1) en daarin was ook de benadering van $\cos(\alpha)\approx1-\tfrac{1}{2}\alpha^2$ gemaakt waarmee de formule uit 1984 gerechtvaardigd kon worden. 

We losten dus $\tan(\alpha)=\alpha+\frac{\varepsilon}{R}$ op via de benadering $\tfrac{1}{3}\alpha^3=\frac{\varepsilon}{R}$:

$$\alpha=\left(\frac{3\varepsilon}{R}\right)^{\tfrac{1}{3}}.$$

De imposante formule hierboven wordt dan

$$h=R\left(\sqrt{1+\tan^2(\alpha)}-1\right).$$

Met nog een benadering: $\sqrt{1+x}=\tfrac{1}{2}x$ voor kleine $x$ wordt het resultaat dan

$$h\approx\frac{R}{2}\tan^2(\alpha)=\frac{R}{2}\left(\alpha+\tfrac{1}{3}\alpha^3\right)^2\approx\frac{R}{2}\alpha^2$$

net als in 1984.

De laatste stap kunnen we rechtvaardigen door het kwadraat uit te schrijven: er komt

$$\frac{R}{2}\left(\alpha^3+\tfrac{2}{3}\alpha^4+\tfrac{1}{9}\alpha^6\right).$$

Reken maar eens na dat met de waarden voor $R$ en $\alpha$ uit 2004 die hogere machten van $\alpha$ maar een paar millimeter bijdragen. Om te zien hoe $h$ van $R$ en $\varepsilon$ afhangt gebruiken we de uitdrukking voor $\alpha$ die we net gevonden hebben:

$$h\approx\frac{R}{2}\left(\frac{3\varepsilon}{R}\right)^{\tfrac{2}{3}}=\frac{3^{\tfrac{2}{3}}}{2}\cdot R^{\tfrac{1}{3}}\cdot\varepsilon^{\tfrac{2}{3}}$$

(vul maar $\varepsilon=\tfrac{1}{2}$ in.)

Hier is een tabelletje met de waarden van $h$ bij $\varepsilon=\tfrac{1}{2}$ voor een paar waarden voor $R$:

$\color{white}{Bron}$	$\color{white}{R}$	$\color{white}{h}$
Tabellenboek 1974	$6\,400\,000\ m$	$121{,}64\ m$
Artikel uit 1984	$6\,378\,000\ m$	$121{,}50\ m$
Artikel uit 2004	$6\,366\,198\ m$	$121{,}43\ m$
Gemiddelde in 2024	$6\,371\,000\ m$	$121{,}46\ m$

(De laatste waarde voor $R$ komt van Wikipedia: Earth Radius.)

In 2004 vroegen we ook te kijken wat er gebeurt als je maar één centimeter touw toevoegt. Kun je het touw zonder hulpmiddelen strak krijgen? We delen dus $\varepsilon$ door $100$. De nieuwe waarde van $h$ is dan

$$\frac{3^{\tfrac{2}{3}}}{2}R^{\tfrac{1}{3}}\frac{\varepsilon^{\tfrac{2}{3}}}{100^{\tfrac{2}{3}}}$$

en dat is het oude antwoord gedeeld door $100^{\tfrac{2}{3}}$.

Hoe groot is $100^{\tfrac{2}{3}}$ ongeveer? We kunnen het ook schrijven als $10000^{\tfrac{1}{3}}=10\cdot10^{\tfrac{1}{3}}$.  Nu geldt $2^3 = 8$ en $10 < 2{,}2^3$ (reken maar na), dus $2<10^{\tfrac{1}{3}}<2{,}2$, ofwel $20 <100^{\tfrac{2}{3}}<22$.

Voor de nieuwe waarde $h′$ van $h$ geldt nu

$$\frac{121}{20}>h'>\frac{121}{22}>5.$$

Je hebt nog steeds een hoge trap nodig om dat touw strak te krijgen en er kan nog steeds een ijsbeer onderdoor. En dat met maar $1\ cm$ extra touw!