Stel je hebt vijf identieke, dus niet van elkaar te onderscheiden, knikkers. Figuur 1 toont alle mogelijke manieren (zeven in totaal) waarop je deze knikkers kunt opdelen in groepjes.

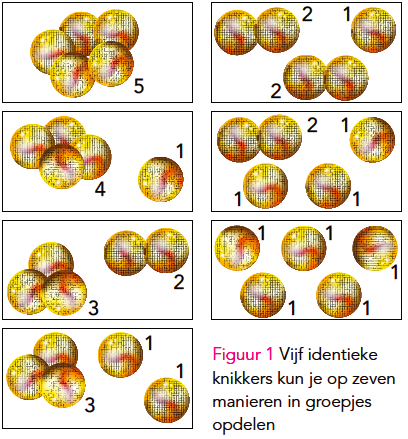
Hebben we zeven knikkers, dan zijn dit enkele van de mogelijkheden: 7, 6 + 1, 5 + 2, 5 + 1 + 1, en het gaat zo nog een tijdje door. Je komt aan vijftien mogelijkheden.

We kunnen natuurlijk altijd door tellen nagaan hoeveel manieren er zijn, maar als je veel knikkers hebt, dan loop je het gevaar dat je de tel kwijtraakt op een bepaald ogenblik. Is er dan misschien een formule om het antwoord te vinden?

Indien we het aantal manieren voor n identieke knikkers noteren als p(n), dan krijgen we een rij getallen waarvan je eenvoudig kunt nagaan dat de eerste termen, beginnend bij n = 1, gelijk zijn aan:

$$p(1) = 1, p(2) = 2, p(3) = 3, p(4) = 5, p(5) = 7, p(6) = 11, p(7) = 15, p(8) = 22, …$$

We spreken verder af dat p(0) = 1. Deze rij wordt de rij van de partitiegetallen genoemd, A000041 in de Online Encyclopedia of Integer Sequences (OEIS). In het woord partitie herken je ‘part’: een deel.

EEN FORMULE

Het probleem om een formule te vinden die voor een gegeven n de waarde van p(n) vindt, gaat al terug tot Gottfried Leibniz, de grote wiskundige en filosoof, die deze vraag in 1674 stelde aan een van de andere wiskundigen van zijn tijd. In figuur 2 zie je enkele berekeningen die zijn teruggevonden in de notities die Leibniz heeft achtergelaten.

Niet Leibniz, maar Leonhard Euler vond een (toch wel merkwaardige) formule die ons toelaat om p(n) te berekenen voor elke n, vertrekkend van de waarde p(0) = 1:

$$p(n) = p(n – 1) + p(n – 2) – p(n – 5) – p(n – 7) + p(n – 12) + p(n – 15) – p(n – 22) – …$$

Het vreemde aan de formule is dat ze eindigt met drie puntjes. Je gebruikt ze als volgt: voor een gegeven n bereken je de termen in het rechterlid en neemt ze samen zoals de formule voorschrijft, waarbij we doorgaan totdat het argument van p negatief wordt. Neem bijvoorbeeld n = 7, dan krijg je:

$$p(7) = p(7 – 1) + p(7 – 2) – p(7 – 5) – p(7 – 7) + p(7 – 12) + p(7 – 15) – p(7 – 22) – …$$

$$= p(6) + p(5) – p(2) – p(0).$$

Je ziet dat je voor de berekening van p(7) de waarden van p(6), p(5), p(2) en p(0) nodig hebt. We hebben afgesproken dat p(0) = 1. En de andere drie kunnen we nu berekenen met diezelfde formule van Euler, maar dan hebben we ook de tussenliggende waarden nodig:

$$p(1) = p(1 – 1) + p(1 – 2) – … = p(0) = 1. $$

$$p(2) = p(2 – 1) + p(2 – 2) – p(2 – 5) – … = p(1) + p(0) = 1 + 1 = 2.$$

$$p(3) = p(3 – 1) + p(3 – 2) – p(3 – 5) – … = p(2) + p(1) = 2 + 1 = 3.$$

$$p(4) = p(4 – 1) + p(4 – 2) – p(4 – 5) – … = p(3) + p(2) = 3 + 2 = 5.$$

$$p(5) = p(5 – 1) + p(5 – 2) – p(5 – 5) – p(5 – 7) + … = p(4) + p(3) – p(0) = 5 + 3 – 1 = 7.$$

$$p(6) = p(6 – 1) + p(6 – 2) – p(6 – 5) – p(6 – 7) + … = p(5) + p(4) – p(1) = 7 + 5 – 1 = 11.$$

$$p(7) = p(6) + p(5) – p(2) – p(0) = 11 + 7 – 2 – 1 = 15.$$

Het werkt! Maar er zijn nog enkele vragen.

MEER DETAILS BIJ EULERS FORMULE

Hoe zit het nu precies met de tekens van de termen in het rechterlid van de formule van Euler? Het gaat inderdaad verder zoals je verwacht: telkens afwisselend twee plustekens en twee mintekens.

 

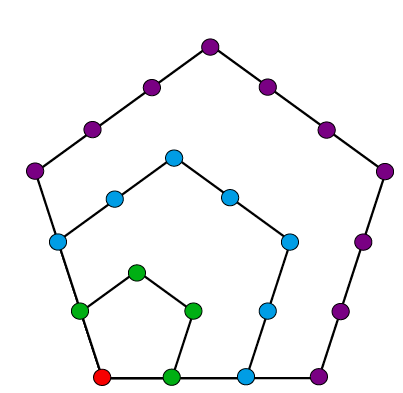
En dan zijn er nog die getallen 1, 2, 5, 7, 12, 15, 22, … in het rechterlid van de formule. Waar komen die vandaan? Zoek je die rij getallen op in de OEIS, dan kom je uit bij A001318, de veralgemeende vijfhoeksgetallen. De gewone vijfhoeksgetallen hebben te maken met vijfhoeken, zoals je kan zien in figuur 3 (zie ook Pythagoras 55-2, aflevering 3 in deze serie over getallenrijen). Het kleinste vijfhoeksgetal is 1, we associëren het met het rode hoekpunt linksonder. Neem je daar de punten op de kleinste vijfhoek bij, dan kom je aan 5, het tweede vijfhoeksgetal. Aangevuld met de punten van de volgende vijfhoek komen we uit op 12, het derde vijfhoeksgetal. En zo gaat het verder: 1, 5, 12, 22, 35, 51, 70, 92, …

Er is een formule voor de berekening van de vijfhoeksgetallen. Het k-de vijfhoeksgetal is gelijk aan

$$\frac{1}{2} k(3k – 1), \ \ \ \ \ k = 1, 2, 3, …$$

Je kan dit eenvoudig zelf vinden, gebruikmakend van de eerste vier, door de ‘IQ-formule’ te gebruiken (zie Pythagoras 48-6). De veralgemeende vijfhoeksgetallen worden vervolgens berekend met dezelfde formule door ook nul en negatieve waarden toe te laten voor k, dus

$$\frac{1}{2} k(3k – 1),\ \ \ \ \ \  k = 0, ±1, ±2, ±3, …$$

De rij van de veralgemeende vijfhoeksgetallen begint dus met 0, 1, 2, 5, 7, 12, 15, 22, 26, …

EULERS BEREKENING

Misschien vraag je je af waar Euler partities zag in zijn formule. Hij redeneerde als volgt (en nu volgt er een heleboel algebra). Het symbool x speelt een grote rol in dit verhaal. We nemen het product van de som van alle machten van x, de som van alle machten van $x^2$, de som van alle machten van x3 enzovoort. Het product in kwestie ziet er zo uit:

$$(1 + x + x^2 + …) · (1 + x^2 + x^4 + …) · (1 + x^3 + x^6 + …) · …$$

Dit product bevat alle informatie over de partitiegetallen en dit wordt duidelijk als we het uitwerken. Dat is een hels werk natuurlijk, en je krijgt iets dat de vorm heeft van een polynoom in x met oneindig veel termen. Aan de hand van een voorbeeld zullen we laten zien waar we naartoe willen.

EEN VOORBEELD

Je kan de waarde van p(5) terugvinden in dit product, en wel als volgt. We gaan op zoek naar de term in het product die $x^5$ bevat. Dan moeten we in elk van de factoren een term kiezen en wel zo dat het product ervan $x^5$ geeft, bijvoorbeeld als je de term $x^2$ neemt in de eerste factor, en de term $x^3$ in de derde factor, en in alle andere factoren kies je de 1, dan vind je $x^5$ als resultaat. Het is wat puzzelen, en laten we dat dan ook even doen. Het is duidelijk dat we in de factoren vanaf de zesde (die begint met 1 + $x^6$) de term 1 moeten nemen in het product, want 6 > 5. We kijken nu even naar de eerste 5 factoren, en schrijven die zo:

$$1 + x^1 + x^{1+1} + x^{1+1+1} + x^{1+1+1+1} + x^{1+1+1+1+1} + …$$

$$1 + x^2 + x^{2+2} + …$$

$$1 + x^3 + …$$

$$1 + x^4 + …$$

$$1 + x^5 + …$$

Nu maken we het product en nemen enkel die termen die als je ze met elkaar vermenigvuldigt x5 geven.

Dit zijn ze:

$$x^1 · x^{2+2}$$

$$x^1 · x^4$$

$$x^{1+1} · x^3$$

$$x^{1+1+1} · x^2$$

$$x^{1+1+1+1+1}$$

$$x^2 · x^3$$

$$x^5$$

(Als we een factor 1 gebruiken, dan schrijven we die niet.) We vinden dus 7 termen. Merk nu op dat als we in deze 7 termen de exponenten van x naast elkaar zetten, we dan dit vinden:

1 + 2 + 2

1 + 4

1 + 1 + 3

1 + 1 + 1 + 2

1 + 1 + 1 + 1 + 1

2 + 3

5

En dat zijn precies de manieren waarop we 5 knikkers kunnen verdelen in groepjes. Dus in die polynoom met oneindig veel termen staat deze term op de zesde plaats:$ … + 7x^5 + …$ En de coëfficiënt 7 die bij $x^5$ staat, geeft het partitiegetal p(5). Je kan zelf op dezelfde manier als boven nagaan dat de oneindige polynoom als volgt begint:

$$1 + x + 2x^2 + 3x^3 + 5x^4 + 7x^5 + …$$

En hier staat dus in feite:

$$p(0) + p(1)x + p(2)x^2 + p(3)x^3 + p(4)x^4 + p(5)x^5 + …$$

Hier staat de genererende functie (waarover het in de vorige Pythagoras ging) van de getallen p(n). We concluderen dat indien we dat enorme product uitwerken, we de partitiegetallen dan gewoon kunnen aflezen in het resultaat.

DE LAATSTE STAP

Euler wist dat je zo’n som van machten van x korter kan schrijven. Voor –1 < q < 1 geldt namelijk dat

$$1 + q + q^2 + q^3 + q^4 + … = \frac{1}{1−q}.$$

Dat dit zo is, kan je zelf nagaan door het product in het linkerlid uit te werken:

$$(1 – q) · (1 + q + q^2 + q^3 + q^4 + …) = 1.$$

Dat heeft voor gevolg dat we het product van Euler, dus

$$(1 + x + x^2 + …) · (1 + x^2 + x^4 + …) · (1 + x^3 + x^6 + …) · …,$$

ook zo kunnen schrijven:

$$\frac{1}{(1−x)·(1−x^2 )·(1−x^3 )·... }.$$

En zo zie je dat het product in de noemer een rol speelt. Werken we dit uit, en dat raden we je niet aan, dan vind je uiteindelijk dit:

$$(1 – x) · (1 – x^2) · (1 – x^3) · … = 1 – x – x^2 + x^5 + x^7 – x^{12} – x^{15} + x^{22} + x^{26} – …$$

Je ziet in het rechterlid de veralgemeende vijfhoeksgetallen op het toneel verschijnen! We zijn er nu bijna, nog een laatste stap. Euler vond dus het volgende:

$$p(0) + p(1)x + p(2)x^2 + p(3)x^3 + p(4)x^4 + … = \frac{1}{1−x −x^2 +x^5 +x^7 −x^{12} −x^{15} +...} .$$

Als we beide leden vermenigvuldigen met de noemer van het rechterlid, dan kunnen we de formule van Euler terugvinden:

$$(p(0) + p(1)x + p(2)x^2 + p(3)x^3 + p(4)x^4 + p(5)x^5 + …) · (1 – x – x^2 + x^5 + x^7 – x^{12} – …) = 1.$$

We bekijken dit even voor n = 5. We gaan op zoek naar de term met $x^5$ in het product in het linkerlid. Er zijn vier producten die leiden tot zo’n term:

$$p(0) · x^5 + p(3)x^3 · (–x^2) + p(4)x^4 · (–x) + p(5)x^5 · 1 = (p(5) – p(4) – p(3) + p(0))x^5.$$

Maar omdat er in het rechterlid geen term staat die $x^5$ bevat, moet dit laatste wel 0 zijn. Dus geldt

$$p(5) = p(4) + p(3) – p(0) $$

en dat is inderdaad wat we vinden als we in de formule van Euler n = 5 kiezen!

ANDERE PARTITIEGETALLEN IN DE OEIS

De rij A000041 is niet de enige rij partitiegetallen die je terugvindt in de OEIS. A000008 bijvoorbeeld is de rij die het aantal partities geeft van n in groepen van 1, 2, 5, of 10. Die rij begint zo:

$$1, 1, 2, 2, 3, 4, 5, 6, 7, 8, 11, 12, …$$

Je kan de termen ervan vinden door dit product uit te werken:

$$(1 + x + x^2 + …) · (1 + x^2 + x^4 + …) · (1 + x^5 + x^{10} + …) · (1 + x^{10} + x^{20} + …).$$

Deze rij geeft het antwoord op de volgende vraag.

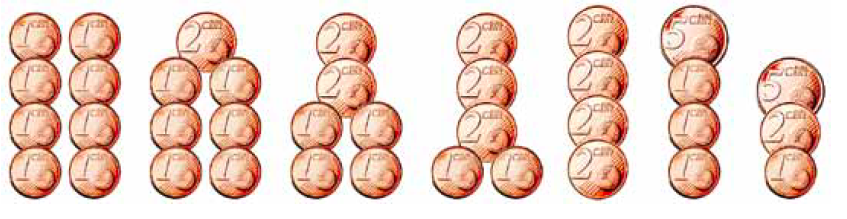
Stel je moet n eurocent wisselgeld geven, en je hebt een onbeperkte voorraad stukken van 1, 2, 5, en 10 eurocent. Op hoeveel manieren kan je dat dan doen? In figuur 4 zie je de oplossingen voor n = 8. In de vorige Pythagoras bespraken we hetzelfde probleem waarbij de muntenvoorraad uit 1- en 2-eurostukken bestaat.

De rij A000009 geeft het aantal partities van n in ongelijke delen. Het getal 5 kun je zo splitsen in 5, 4 + 1 en 3 + 2. Ook deze rij kan je verbinden met een product:

$$(1 + x) · (1 + x^2) · (1 + x^3) · (1 + x^4) · (1 + x^5) · …$$

Zie je waarom? Diezelfde rij geeft blijkbaar ook het aantal partities van n in oneven getallen: 5 kun je splitsen in 5, 3 + 1 + 1 en 1 + 1 + 1 + 1 + 1. Het bijhorende product ziet er nu zo uit:

$$(1 + x + x^2 + …) · (1 + x^3 + x^6 + …) · (1 + x^5 + …) · … = \frac{1}{(1−x)·(1−x^3 )·(1−x^5 )·...} .$$

Euler bewees inderdaad al in 1748 dat deze 2 rijen aan elkaar gelijk zijn. Dit is zijn bewijs:

$$(1 + x) · (1 + x^2) · (1 + x^3) · (1 + x^4) · (1 + x^5) · … =\frac{1}{(1−x)·(1−x^3 )·(1−x^5 )·...} .$$

Ga zelf na dat dit klopt door beide leden te vermenigvuldigen met de noemer rechts, en dan uitgebreid het merkwaardig product $(a – b)(a + b) = a^2 – b^2$ te gebruiken!

PARTITIES VAN N IN ONGELIJKE DELEN

De rij A000009 zegt dat het aantal partities van een getal n in ongelijke delen gelijk is aan het aantal partities in oneven delen. Naast het bewijs van Euler waarmee dit artikel afsluit, is er ook een meer aanschouwelijke manier om dit aan te tonen. We maken hierbij gebruik van de volgende eenvoudige eigenschap van natuurlijke getallen: elk natuurlijk getal is op een unieke manier te schrijven als een macht van 2 maal een oneven getal. Bijvoorbeeld: $98 = 2^1 · 49$, en $2176 = 2^7 · 17.$

Een partitie in ongelijke delen kan nu als volgt eenduidig worden omgezet in een partitie met oneven stukken, en omgekeerd. We doen het met een voorbeeld, de volgende partitie van 20: 20 = 7 + 6 + 4 + 2 + 1.

1. Schrijf elk van de ongelijke delen als een macht van 2 maal een oneven getal: $20 = 2^0 · 7 + 2^1 · 3 + 2^2 · 1 + 2^1 · 1 + 2^0 · 1.$
2. Lees dan af wat er staat: 1 maal 7 + 2 maal 3 + 4 maal 1 + 2 maal 1 + 1 maal 1. Zo hebben we 20 geschreven als 7 + 3 + 3 + 1 + 1 + 1 + 1 + 1 + 1 + 1, een som met enkel oneven getallen.

Ga zelf na hoe het omgekeerd verloopt: met welke som van ongelijke getallen komt de volgende partitie van 20 met oneven delen overeen?

$$20 = 3 + 3 + 3 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1.$$

Een tip: $20 = (2^1 + 2^0) · 3 + (2^3 + 2^1 + 2^0) · 1.$

Pas hetzelfde toe op $$20 = 7 + 3 + 3 + 1 + 1 + 1 + 1 + 1 + 1 + 1,$$ en laat zien dat dit opnieuw 20 = 7 + 6 + 4 + 2 + 1 oplevert.