De kleine spiegel

De kwadraten van 0 tot en met 10 ken je natuurlijk:

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100. (*)

Zie je hier al een mooie eigenschap? Schrijf alleen de laatste cijfers maar eens op en je zult het zien:

0, 1, 4, 9, 6, 5, 6, 9, 4, 1, 0.

De getallen vormen een gespiegelde reeks, met 5 als middelpunt. Vanwege deze spiegeleigenschap eindigen bijvoorbeeld de kwadraten van 1 en 9 op hetzelfde cijfer: 1. Als laatste cijfer ontbreken 2, 3, 7 en 8. Deze vier ontbrekende cijfers liggen ook, als gaten van de gespiegelde reeks, gecentreerd met als middelpunt de 5.

Hoe kun je die spiegelsymmetrie verklaren? Neem bijvoorbeeld de 6 als laatste cijfer. Schrijf 4 als 5 – 1 en 6 als 5 + 1. We passen de merkwaardige producten $(a+b)^2=a^2+2ab+b^2$ en $(a-b)^2=a^2-2ab+b^2$ toe. Kwadrateren van 5 – 1 en 5 + 1 geeft

(5 + 1)² = 25 + 10 + 1 = 25 + 1 + 10 = 36 

en

(5 – 1)² = 25 – 10 + 1 = 25 + 1 – 10 = 16.

Ook met een ander eindcijfer dan 6 is de waarde van $a$  in de merkwaardige producten gelijk aan 5. Daarom zal de factor 2$ab$ telkens een tienvoud zijn. Daarom zijn de gespiegelde getallen in de reeks (*) altijd een even aantal tientallen van elkaar verwijderd: 16 en 36 verschillen 2 tientallen van elkaar, 9 en 49 verschillen 4 tientallen, 4 en 64 verschillen 6 tientallen en 1 en 81 verschillen 8 tientallen.

Het verschil tussen opeenvolgende kwadraten

Wat is het verschil tussen het kwadraat van 8 en 7? Er geldt 64 – 49 = 15. Hé, dit is de som van 7 en 8. Net zo is het verschil van het kwadraat van 9 en 8 gelijk aan 9 + 8. Dit blijkt uit $$(a+1)^2-a^2=a^2+2a+1-a^2=2a+1=a+(a+1).$$

Als we de verschillen tussen twee opeenvolgende kwadraten van 0 tot en met 10 in een reeks zetten, ontstaat de volgende reeks:

1, 3, 5, 7, 9, 11, 13, 15, 17, 19.

Zo is het verschil tussen ¹² (= 1) en 2² (= 4) de som van 1 en 2, en 19 = 9 + 10 is het verschil tussen 9² (= 81) en 10² (= 100). Dit kunnen we gebruiken om 11² te berekenen: 100 + (10 + 11) = 121.

De kleine spiegel voortgezet

De kleine spiegel keert steeds terug bij elke volgende serie van tien. Zo eindigen ook de kwadraten van 10 tot en met 20 op dezelfde reeks als die we hierboven zagen:

100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400.

Dat is geen toeval: het laatste cijfer van een product van twee getallen wordt bepaald door het laatste cijfer van die twee getallen.

Kwadraten van vijf- en tienvouden

De kwadraten van 10, 20, 30, …, 100 zijn simpel: ze zijn gelijk aan de kwadraten van 1 tot en met 10 met twee nullen erachter. Ook de kwadraten van de vijfvouden (die geen tienvoud zijn), zijn niet moeilijk. We nemen 35² als voorbeeld. Neem het eerste cijfer en vermenigvuldig dat met het getal dat 1 groter is: 3 × 4 = 12. Zet daarachter 25 (het kwadraat van 5) et voilà, je hebt de uitkomst: 35² = 1225. Net zo: 85² = 7225.

Waarom werkt deze truc? Het vijfvoud waarvan je het kwadraat wilt berekenen, kun je schrijven als $10a + 5$; er geldt: $$(10a+5)^2=100a^2+100a+25=100a(a+1)+25.$$

Je herkent hier $a(a+1)$ en bovendien zie je dat het getal 25 in al deze kwadraten terugkeert.

De grote spiegel

Als je eerst zelf wilt ontdekken wat we met de ‘grote spiegel’ bedoelen, schrijf dan alle kwadraten van 0 tot en met 50 onder elkaar op en zoek dan naar de regelmaat in de laatste twee cijfers van al deze 51 kwadraten.

Bij de kleine spiegel stond het getal 5 in het centrum. Bij de grote spiegel staat 25 in het midden. Wat blijkt namelijk? Elk kwadraat van een getal dat n onder 25 ligt, eindigt op dezelfde twee cijfers als het getal dat n boven 25 ligt. Neem bijvoorbeeld n = 1: 24² = 576 en 26² = 676. Voor n = 12 geldt op dezelfde manier: (25 – 12)² = 13² = 169 en (25 + 12)² = 37² = 1369.

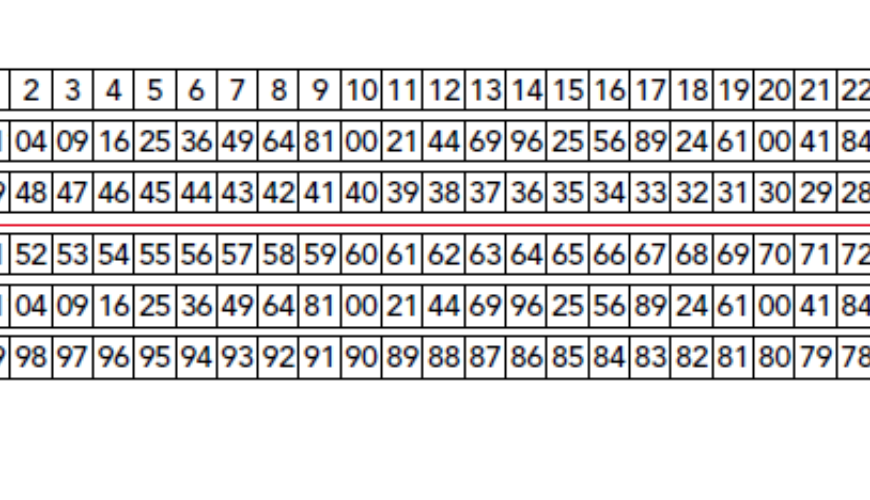
Deze eigenschap zie je onmiddellijk terug in figuur 1. De bovenste rij bevat de getallen van 0 tot en met 25. De rij daaronder geeft de laatste twee cijfers van de kwadraten en in de onderste rij staan – aflopend – de getallen van 50 tot en met 25. Je ziet, bijvoorbeeld, dat de kwadraten van 22 en van 28 beide eindigen op 84. (Die kwadraten zijn 484 en 784.)

Leer de middelste rij in figuur 1 – in beide richtingen – uit het hoofd. Als je nu bijvoorbeeld 49² wilt berekenen, weet je alvast dat het kwadraat eindigt op 01. Bovendien moet dit kwadraat bijna 100 (namelijk 49 + 50) minder zijn dan 2500, het kwadraat van 50. Dus: 49² = 2401.

De verklaring van de symmetrie rond 25 is als volgt:

(25 + $\bm{n}$)² – (25 – $\bm{n}$)² =
(625 + 50$n$ + $n^2$) – (625 – 50$n$ + $n^2$) =
(625 – 625 + $n^2$ - $n^2$ + 100$n$ = 100$n$.

Het verschil tussen de spiegelgetallen is dus altijd exact een honderdvoud, waaruit volgt dat de eenheden en tientallen van beide kwadraten gelijk zijn.

De grote spiegel voortgezet

Net zoals de kleine spiegel zich van tiental tot tiental herhaalt, herhaalt ook de grote spiegel zich steeds, maar dan van vijftigtal naar vijftigtal. Dat betekent dat de lange reeks van laatste twee cijfers van de kwadraten van 0 tot en met 25 ook geldt voor de kwadraten van de getallen 50 tot en met 75, 100 tot en met 125 en bijvoorbeeld ook 300 tot en met 325.

Omdat de laatste twee cijfers van de kwadraten van 25 tot en met 50 worden gevormd door de omgekeerde reeks van de laatste twee cijfers van de kwadraten van 0 tot en met 25, geldt dat dus ook voor de kwadraten van 75 tot en met 100, 125 tot en met 150 en bijvoorbeeld ook 925 tot en met 950.

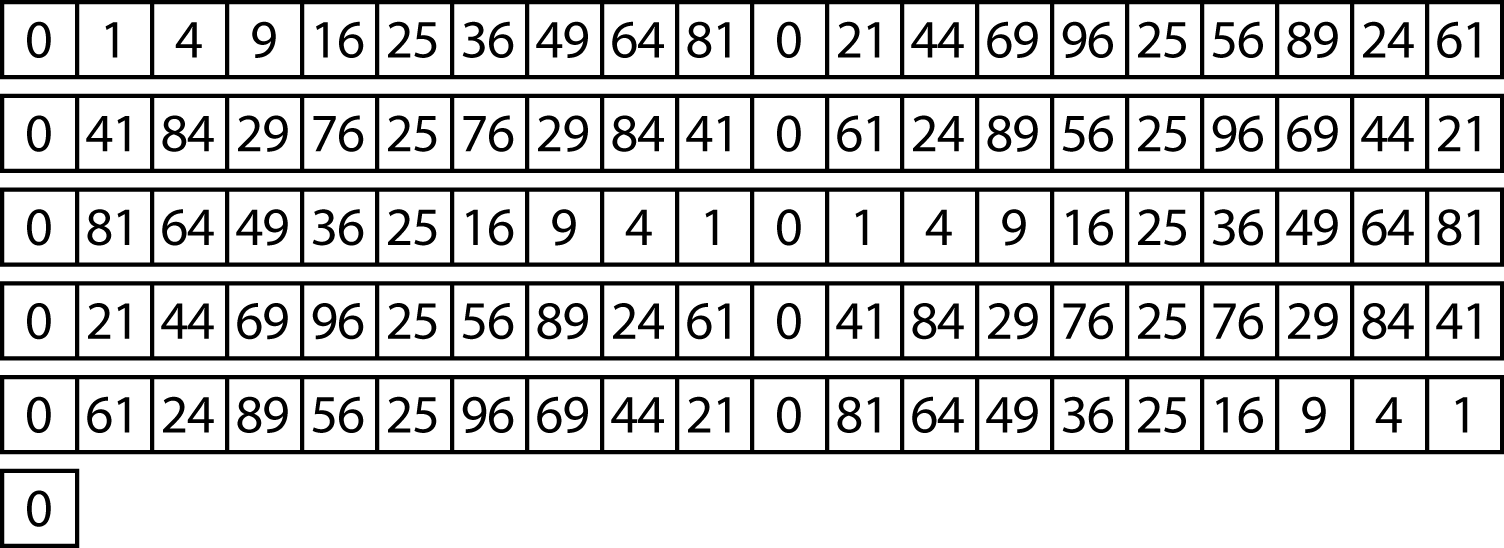
In figuur 2 staan de eindcijfers van de kwadraten van 0 tot en met 100. Daarin zie je bijvoorbeeld dat de kwadraten van 24, 26, 74 en 76 op dezelfde twee cijfers eindigen, namelijk op de cijfers 76 (576, 676, 7476, 7676). Ook de kwadraten van bijvoorbeeld 18, 32, 68 en 82 hebben dezelfde twee eindcijfers: 24 (324, 1024, 4624, 6724). Elk getal onder de 100 dat niet op 0 of 5 eindigt, heeft telkens drie bondgenoten, waarvan de kwadraten op dezelfde twee cijfers eindigen.

De verklaring volgt uit $$(n+50)^2-n^2=100n+2500=100(n+25).$$

Het verschil tussen de kwadraten van $n$ en $n + 50$ is dus exact een honderdvoud, waaruit volgt dat de eenheden en tientallen van beide kwadraten gelijk zijn.

De grote spiegel toegepast

De kwadraten van 1 tot en met 9 kan iedereen moeiteloos noemen. Dat betekent dat ook de laatste twee cijfers van de kwadraten van de drie ‘bondgenoot’-series, namelijk de kwadraten van 51 tot en met 59, 49 tot en met 41 en 99 tot en met 91, geen problemen zullen opleveren. We gaan eerst deze kwadraten helemaal uit ons hoofd leren.

Ten eerste geldt: 50² = 2500 en 60² = 3600. De kwadraten van 51 tot en met 59 liggen tussen 2500 en 3600 in, en wel op de volgende manier:

2500, 2601, 2704, 2809, 2916, 3025, 3136, 3249, 3364, 3481, 3600.

Voor elk kwadraat van $50 + n$ (met $n < 10$) geldt dus dat het honderdtal 25 wordt verhoogd met $n$. Vervolgens wordt er $n^2$ (01, 04, 09, …, 81) bij opgeteld. Bijvoorbeeld: 54² = 2500 + 400 + 16 = 2916 en 56 = 2500 + 600 + 36 = 3136.

Terugtellend van 49 tot 41 eindigen ook deze kwadraten weer op de kwadraten van 1 tot en met 9. Dus 49² = 2401, 48² = 2304, …, 41² = 1681. Omdat we bij deze kwadraten moeten terugrekenen vanaf 2500, ligt bijvoorbeeld 46² vier honderdtallen onder de 2500 met daarbij opgeteld 4² (dus weer twee keer de factor 4). Het kwadraat van 42 (= 50 – 8) ligt dus acht honderdtallen onder de 2500 met daarbij opgeteld 8²: 2500 – 800 + 64 = 1764. De kwadraten van 40 tot en met 50 zijn dus:

1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500.

Je kunt bij deze kwadraten ook eventueel rekenen vanaf 1600, maar dan moet je je ervan bewust zijn dat het honderdtal van bijvoorbeeld 42² niet twee honderdtallen, maar slechts één honderdtal boven dat van 1600 ligt. De oorzaak hiervan is dat 40² en 41² beide 16 honderdtallen bevatten. Dus 43² = 1849 = (25 – 7)100 + 7² = (16 + 3 – 1)100 + 7².

Het uit het hoofd leren van de kwadraten van 91 tot en met 99 verloopt parallel met die van 41 tot en met 49. Waar deze laatste onder de 2500 lagen, liggen de kwadraten van 91 tot en met 99 onder de 10000. Elk kwadraat is telkens 200 minder dan het vorige met daarbij het bijbehorende kwadraat opgeteld. Dus 99² = 9801, 98² = 9604, …, 91² = 8281. De kwadraten van 90 tot en met 100 zijn dus:

8100, 8281, 8464, 8649, 8836, 9025, 9216, 9409, 9604, 9801, 10000.

Merk ook hier weer op dat 8281 slechts één honderdtal boven de 8100 ligt, en niet twee honderdtallen.

Misschien ken je de kwadraten van 11 tot en met 14 al uit je hoofd. Zo niet, leer ze dan even: 121, 144, 169 en 196. Je ziet: ze liggen allemaal tussen de 100 en de 200. Met andere woorden: hun honderdtal verandert niet (ten opzichte van 10²).

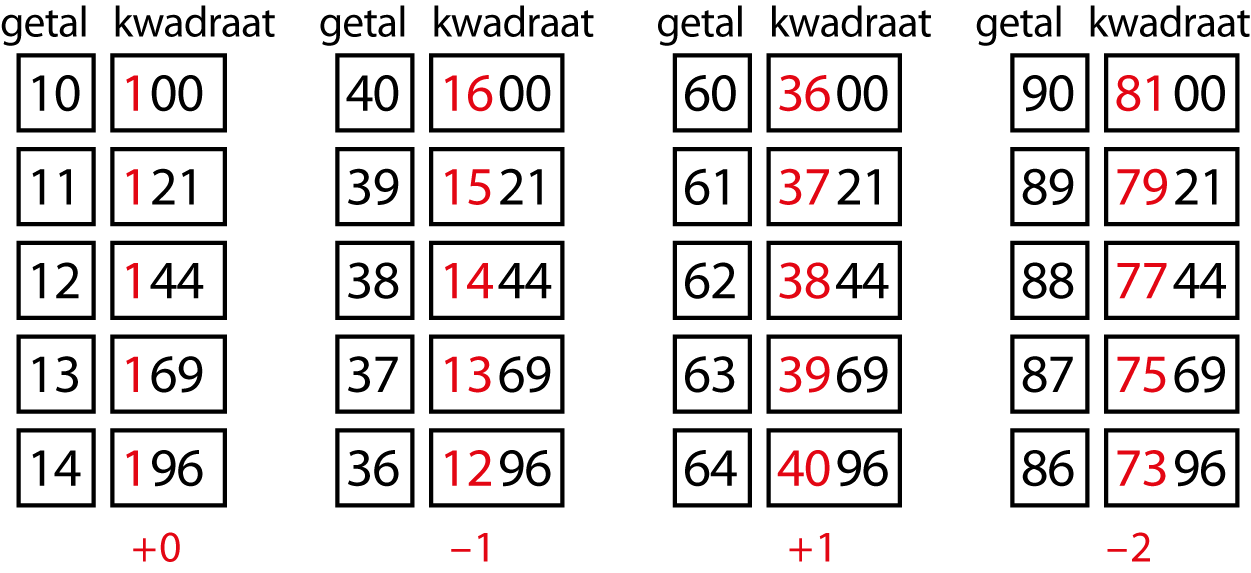
In figuur 3 zie je deze kwadraten samen met die van hun bondgenoten onder de 100. Zoals gezegd, verandert het honderdtal in kolom 1 niet (ten opzichte van 100). In kolom 2 wordt het honderdtal telkens 1 minder (ten opzichte van 1600), in kolom 3 wordt het honderdtal telkens 1 meer (ten opzichte van 3600) en in kolom 4 wordt het honderdtal telkens 2 minder (ten opzichte van 8100).

We geven een paar voorbeelden. Het kwadraat van 37 eindigt op 69 en het honderdtal is 16 – 3 = 13. Dus 37² = 1369. Het kwadraat van 62 eindigt op 44 en het honderdtal is 36 + 2 = 38. Dus 62² = 3844. Het kwadraat van 86 eindigt op 96 en het honderdtal is 81 – (2 × 4) = 73. Dus 86² = 7396.

Natuurlijk is het ook mogelijk om het honderdtal van 86² ten opzichte van 85² = 7225 te bepalen; dan wordt het honderdtal van 86² (bijna) vanzelfsprekend 73, omdat 86² = 85² + 85 + 86 = 7396.

Het restant

Zo, je kent nu 68 kwadraten uit je hoofd. Nog 32 te gaan, en dan ken je alle kwadraten tot en met dat van 100 van buiten. De 32 kwadraten die we nog niet kennen, zijn die van 16 tot en met 19 en 21 tot en met 24, en hun bondgenoten. Hier maken we drie groepjes van.

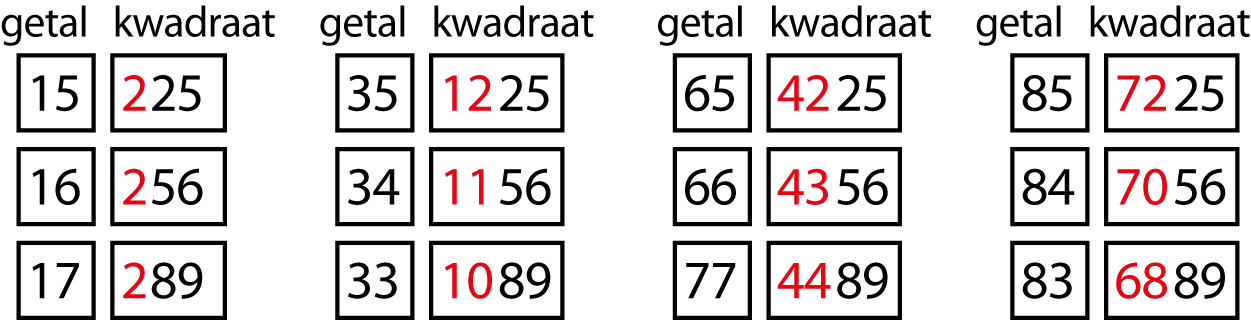
We beginnen met 16 en 17, en hun bondgenoten. De kwadraten van deze getallen relateren we aan die van 15 en zijn bondgenoten: zie figuur 4. Natuurlijk is het ook mogelijk om het kwadraat van 83 ten opzichte van 80² te bepalen: (80 + 3)² = 6400 + 3 × 160 + 9 = 6889. Vanzelfsprekend eindigt dit kwadraat op 89.

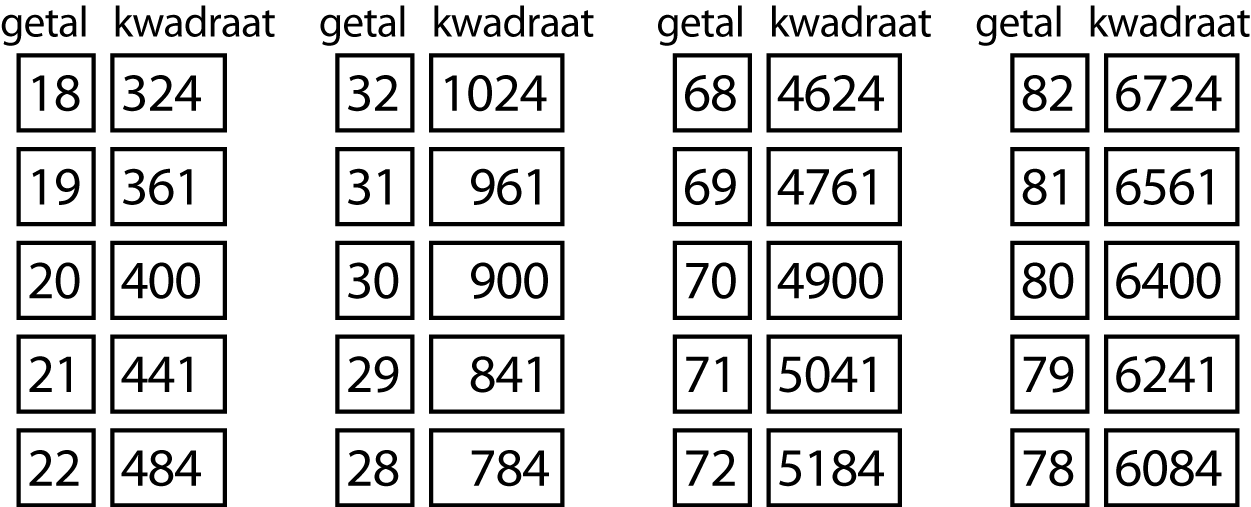
Dan 18, 19, 21 en 22, en bondgenoten. De kwadraten van deze getallen relateren we aan die van 20 en zijn bondgenoten: zie figuur 5. Merk op dat de kwadraten van 19 en bondgenoten niet in dit systeem passen. De verschillen tussen de honderdtallen van deze kwadraten en de kwadraten van aangrenzende tientallen verschillen alle 1 meer dan geldt voor de rest van de kolom. Dus het verschil in honderdtallen tussen de kwadraten van twee aangrenzende getallen in kolom 1 is telkens 0, met uitzondering van 19² en 20². In dat geval is het verschil 1 meer, namelijk 1. Dit is logisch, omdat 400 het kleinste getal is met honderdtal 4. Vanzelfsprekend is 19² dan gelijk aan 361 (= 400 – 20 – 19).

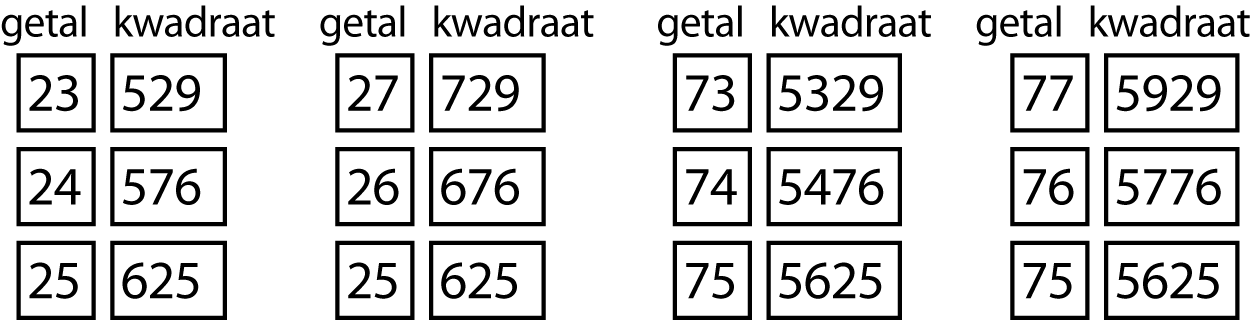
Tot slot 23 en 24, en bondgenoten. Hun kwadraten relateren we aan die van 25 en zijn bondgenoten: zie figuur 6. Deze kwadraten liggen alle dichtbij de middelpunten 25 en 75. Daardoor kunnen deze kwadraten gemakkelijk met elkaar in verband worden gebracht.

De getallen 576 en 676 verschillen 100 (= 2 × 50) van elkaar, met 625 bijna precies in het midden ertussen. De getallen 529 en 729 verschillen 200 (= 4 × 50) van elkaar, met 625 eveneens bijna in het midden. Dit geldt ook voor de kwadraatparen van 73, 77 en 74, 76, maar dan met 5625 in het midden. De getallen 5476 en 5776 verschillen 300 (= 4 × 75) van elkaar. En de getallen 5329 en 5929 verschillen 600 (= 8 × 75) van elkaar.