In het artikel ‘Losse eindjes’ (Pythagoras 55-6, juni 2016) maakten we gebruik van invarianten: holle ruimtelijke figuren die na het binnenstebuiten keren weer dezelfde figuren opleveren. Vervolgens plaatsten we piramides op de invarianten zodat het grondvlak van iedere piramide samenviel met een zijde van de invariant. De hoogte van de piramides is hierbij van groot belang. Na omkering van de invarianten moeten de piramides namelijk in de invarianten passen. Om de invarianten om te kunnen keren, maakten we er uitslagen van in de vorm van een lint. Ieder vlak zit dan aan twee andere vlakken bevestigd, behalve de twee buitenste natuurlijk. Hierbij moest ieder vlak op dezelfde manier aan twee andere vlakken worden bevestigd.
In dit artikel willen we niet gebruikmaken van een lint als uitslag van de invarianten, maar van een gesloten band. Wat je je dan kunt afvragen, is of het mogelijk is om de linten te gebruiken en dan de uiteinden aan elkaar bevestigen. Met de drie invarianten die eerder zijn besproken (tetraëder, octaëder en kubus) lukt dit niet. Je kunt dit eenvoudig nagaan door de uitslagen op papier te tekenen, uit te knippen en vervolgens de uiteinden aan elkaar bevestigen.
Een van de redenen waarom dit omkeren niet lukt, is dat er niet voldoende ruimte is. De band moet geleidelijk door het binnenste van deze zelfde band worden gehaald en daar is ruimte voor nodig. We zullen dus extra ruimte moeten creëren. Hoe we dit gaan doen bespreken we later. Wat verder van belang is om een invariant om te kunnen keren, is de rangschikking van de vlakken ten opzichte van elkaar en het aantal vlakken waaruit de invariant bestaat.

Figuur 1

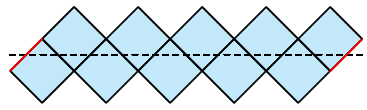
Figuur 2

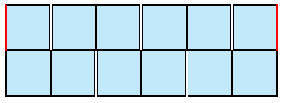
Afbeelding 3

De figuren 1, 2 en 3 zijn niet allemaal uitslagen van ruimtelijke figuren, het zijn slechts gesloten banden. Hiermee willen we alleen maar verduidelijken dat de rangschikking van de vlakken, de ruimte en het aantal vlakken van belang is. De rode lijnen in de figuren geven aan waar en hoe de uiteinden aan elkaar moeten worden bevestigd. Met de uitslag in figuur 1 krijgen we een band die je niet kunt omkeren. Als we hetzelfde zouden doen met bijvoorbeeld 20 vierkanten, dan kan je de band nog steeds niet omkeren zonder de vlakken te vervormen. Er is dan weliswaar voldoende ruimte om de band om te kunnen keren, maar door de rangschikking van de vlakken gaat het toch niet. De vouwlijnen van de vierkanten staan immers loodrecht op de lange zijden van de band en daardoor kan je alleen maar in de lengerichting van de band vouwen. Met een andere rangschikking van de vierkanten (figuur 2) kan met 10 vierkanten een omkeerbare band worden gemaakt. Nu staan de vouwlijnen van de vierkanten onder een hoek van 45 graden ten opzichte van het hart van de band (stippellijn). Trouwens, met minder dan 10 vierkanten gaat het omkeren niet, omdat er dan niet voldoende ruimte is. In figuur 3 zie je een uitslag waarbij, net als in figuur 1, de vierkanten op dezelfde manier ten opzichte van de lengterichting van de band zijn gerangschikt. Ze zijn echter wel op een andere manier aan elkaar bevestigd. De vouwlijnen lopen evenwijdig en loodrecht op de lengterichting van de band. Door de evenwijdige vouwlijn en de rangschikking van de vlakken is de band omkeerbaar.
Ook de vorm van de delen speelt een rol bij het kunnen keren van een band. Tot nu toe hebben we alleen maar vierkanten gezien, maar met bijvoorbeeld gelijkzijdige driehoeken kunnen we vergelijkbare dingen doen.
Bij de constructies die we gaan maken, zijn we gebonden aan het aantal vlakken van de invariant. We kunnen dus niet zomaar een paar extra vlakken toevoegen, want dit zou de vorm van de invariant veranderen. We kunnen de vlakken wel in kleinere vlakken snijden en de vlakjes op een andere manier rangschikken. Natuurlijk moet dit zo gebeuren dat nog steeds de invariant kan worden gemaakt en dat een gesloten band kan worden gevormd.

De snijmethode

In het artikel ‘De binnenkant van de tetraëder’ (Pythagoras 55-1, september 2016) bespraken we de ‘snijmethode’. De vlakken van de tetraëder sneden we doormidden zodat rechthoekige driehoeken onstaan. Zo kan de oorspronkelijke uitslag, bestaande uit vier gelijkzijdige driehoeken, worden omgevormd tot een uitslag bestaande uit 8 rechthoekige driehoeken. Vervolgens werd met de uitslag een gesloten band gemaakt.
In ‘Losse eindjes’ in de vorige Pythagoras legden we uit dat we bij een lint (dit is de uitslag van de invariant) alle vlakken zoveel mogelijk dezelfde eigenschap willen geven. Verbinden we de twee uiteinden aan elkaar, zodat een band ontstaat, dan willen we ook dat de twee buitenste vlakken van het lint dezelfde eigenschap hebben. Dit betekent voor een lint zonder losse flapjes dat ieder tussenliggend vlak aan precies twee andere vlakken grenst. Maken we van het lint een band, dan geldt dit voor alle vlakken.
Gaan we vervolgens vlakken in kleinere vlakken snijden, dan ontstaan nieuwe zijden. Hieraan kunnen geen vlakken worden bevestigd. Alleen het deel dat eerst aan het vlak vast zat, zou hieraan kunnen worden bevestigd, maar dan krijg je het oorspronkelijke vlak terug. Er kan alleen maar aan één van de al bestaande zijden een andere al bestaande zijde worden gekoppeld. Om zo een lint of band te kunnen vormen, moet je bij het snijden van de kleinere vlakken rekening houden met het feit dat er minstens twee zijden van het oorspronkelijke vlak aanwezig zijn. Bij slechts één oorspronkelijke zijde kan dus maar één ander vlak aan het vlak worden bevestigd en dan kan geen lint of band worden gevormd.
We gaan er bij de snijmethode van uit dat de invariant uit gelijkzijdige veelhoeken bestaat. Niet alle vlakken hoeven noodzakelijk te bestaan uit evenveel zijden. Dit is afhankelijk van de ruimtelijke figuur (dit is de invariant). Nu kan een vlak op verschillende manieren in kleinere vlakken worden gesneden. Hierbij willen we dat de vlakjes zoveel mogelijk gelijke vormen krijgen of dat ze gespiegeld zijn ten opzichte van elkaar. Het snijden van een vlak kan beginnen in een hoek of in het midden van een zijde en de snede eindigt in het zwaartepunt van het vlak. Er zijn zo minstens twee snedes nodig om een vlak in kleinere vlakjes te verdelen. Twee snedes kunnen een rechte lijn vormen, maar dit hoeft niet.
Als je in het midden van een zijde begint met snijden, dan zal het aangrenzende vlak, dat dus een ribbe deelt, ook een snede moeten hebben die begint in het midden van dezelfde ribbe.

Figuur 4, 5, 6, 7 en 8

Zijn de oorspronkelijke vlakken bijvoorbeeld gelijkzijdige driehoeken, dan kun je die zo snijden, dat twee gespiegelde rechthoekige driehoeken ontstaan (zie figuur 4). Als je de gelijkzijdige driehoeken in drie gelijke delen wilt snijden, dan kan dat door vanuit iedere hoek naar het zwaartepunt te snijden. Maar dan kan geen lint of band worden gevormd, omdat er dan slechts één oorspronkelijke zijde is overgebleven en hier kan maar één ander vlak aan worden bevestigd. Driehoeken kunnen ook nog anders worden gesneden. Door vanuit de middens van de zijden te snijden, ontstaan drie vliegers (zie figuur 5). Iedere vlieger heeft dan twee originele zijden. Hiermee kan dan mogelijk wel een lint of band worden gevormd.
Zo kan bijvoorbeeld een vierkant over een diagonaal doormidden worden gesneden (twee snedes; zie figuur 6). Dan ontstaan twee gelijkbenige driehoeken. Ook dan heeft ieder deel twee originele zijden. Een vierkant kan ook zo doormidden worden gesneden, dat twee rechthoeken ontstaan (zie figuur 7). Dan heeft ieder deel drie originele zijden. Een vierkant kan ook in vier kleinere vierkanten worden gesneden (zie figuur 8). Ook dan heeft ieder deel twee originele zijden. Op soortgelijke wijze kun je vijfhoeken, zeshoeken of andere willekeurige n-hoeken snijden.
De snijmethode werkt het beste als je vanuit de ruimtelijke figuur werkt en niet vanuit de uitslag met de oorspronkelijke, gelijkzijdige vlakken, omdat in de ruimtelijke figuur duidelijker is te zien hoe je de vlakken moet snijden om tot een lint of band als uitslag te komen.

 

De constructiemethode

Eigenlijk is de constructiemethode niets anders dan de methode die we in het vorige nummer bespraken. We gebruiken dezelfde principes als voorheen. We hebben een invariant en hierop plaatsen we consequent aan een zijde of beide zijden piramides op alle vlakken. We moeten nu echter rekening houden met het feit dat vlakken tot kleinere vlakken zijn versneden. Dat betekent dat de piramides ook tot kleinere objecten moeten worden versneden. De snedes van het grondvlak van de piramides moeten samenvallen met de snedes van de invariant. Daarna worden de piramides loodrecht op hun grondvlak doorgesneden

 

Van tetraëder naar triakistetraëder

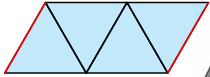
Figuur 9

In figuur 9 zie je een gebruikelijke uitslag van een tetraëder. Als de twee rode zijden aan elkaar worden bevestigd, dan ontstaat meteen de tetraëder. Er is geen ruimte om de tetraëder om te keren. We gaan kijken welke mogelijkheden er zijn voor het snijden van de vlakken.
We kunnen, zoals we hebben gezien, vlakken in tweeën snijden (zie figuur 4) of in drieën (zie figuur 5). Als we alle vlakken in drieën snijden, kunnen we geen uitslag maken die uit één geheel bestaat. Er ontstaan zo vier losse delen. Als drie vlakken in drieën worden gesneden, dan moet het laatste vlak ook in drie delen worden gesneden, omdat drie snedes van de andere vlakken uitkomen bij dit ene vlak. En iedere snede moet dan doorlopen. Als we twee van de vier vlakken in drieën snijden, dan moeten ook de andere twee vlakken in drieën worden gesneden. Dit heeft opnieuw te maken met het feit dat een snede in het ene vlak moet doorlopen in het andere vlak. Als we slechts een vlak in drieën snijden, dan is het mogelijk om de overige vlakken in tweeën te snijden. Maar ook dan kunnen we geen uitslag uit een geheel maken. Dit komt omdat de sneden die de drie vlakken in tweeën snijden, samenkomen in een hoek van de tetraëder. Zo ontstaan drie losse delen. We kunnen wel alle vlakken in tweeën snijden en zo een aaneengesloten uitslag maken (zie figuur 10 en 11). In figuur 10 is met blauwe lijnen aangegeven hoe je de vlakken moet snijden en verder is aangegeven hoe de piramide (in rood) in de tetraëder past. In figuur 11 zie je de uitslag. Als we de rode zijden aan elkaar bevestigen, krijgen we een band waarmee we de tetraëder kunnen vormen, maar zoals we al eerder hebben gezien (Pythagoras 55-1) is de band zo niet om te keren. Daarvoor zouden we extra vouwlijnen moeten aanbrengen. En dit werkt alleen maar voor een band zonder dikte.

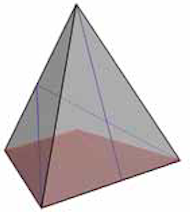
Figuur 10

Figuur 11

Als we piramides op de invariant zouden plaatsen, dan kan het omkeren niet meer. Maar we gaan toch piramides op de invariant plaatsen en gebruiken het lint zoals in figuur 11; met andere woorden, we maken er geen gesloten band van. De piramides moeten doormidden worden gesneden om ze op de rechthoekige driehoeken te laten passen. Om de halve piramides te kunnen maken, hebben we de snedelengtes nodig in de piramide. In figuur 10 is de snede in de piramide te zien. In de vorige Pythagoras hebben we de lengte van de topribben van de piramides al bepaald. Alleen de snedelengtes door het grondvlak en door een van de zijvlakken van de piramide zijn nog niet bekend. Maar omdat we de lengte weten van de zijden van het grondvlak (die hebben we zelf gekozen en hadden we 2 genomen) en de lengtes van de topribben ( $\frac{1}{2}\sqrt{6}$), kun je eenvoudig de lengte van de snedes bepalen. In figuur 4 zie je de situatie waarbij het grondvlak doormidden wordt gesneden. Met de stelling van Pythagoras vind je dan de lengte van de snede – dit rekenwerk laten we aan jezelf over.
In figuur 12 zie je een zijvlak van een piramide met de bekende lengtes. De waarde van $s$ kennen we nog niet, maar die kun je ook zelf met de stelling van Pythagoras berekenen. Het kan trouwens ook anders, zonder gebruik te maken van de ribbenlengtes (gebruik de kubus als hulpmiddel – het blijkt dat s de halve hoogte van de kubus is).

Figuur 12, 13 en 14

Van kubus naar rombendodecaëder

Van de kubus is in figuur 13 een gebruikelijke uitslag gegeven. Hiermee is geen omkeerbare band te maken. Als we hier de rode zijden aan elkaar bevestigen, ontstaat meteen de kubus. En er is dan geen ruimte voor het omkeren. Om dit mogelijk te maken, zullen we de vlakken in kleinere vlakken moeten snijden. Dat kan op een aantal manier snijden. Zoals we zagen, kan een vlak in vier kleinere vierkanten worden gesneden of in twee rechthoeken of in twee rechthoekige driehoeken. Natuurlijk kan een vlak nog op andere manieren worden gesneden, bijvoorbeeld als in figuur 14, maar dan krijgen we te veel verschillen en dat willen we niet. Het is mogelijk om alle vlakken in twee rechthoeken te snijden en zo een aaneengesloten lint te maken. Maar dan moet nog extra over vier ribben worden gesneden. En hiermee kun je een band maken die omkeerbaar is. We bespreken deze manier hier niet, omdat er een extra eis wordt gesteld bij het snijden. Wel bespreken we de manier waarbij alle vlakken in rechthoekige driehoeken worden gesneden. Daarmee is ook een gesloten band te maken.
We nemen een willekeurige hoek van de kubus. Deze hoek wordt gevormd door drie vierkanten. Vanuit deze hoek snijden we vervolgens de drie vlakken diagonaalsgewijs. We doen hetzelfde bij de hoek die op de dezelfde hoofddiagonaal van de kubus ligt. Dus ook hier worden vanuit de hoek de drie vlakken diagonaalsgewijs gesneden. In figuur 15 hebben we in blauw aangegeven hoe we de kubus moeten snijden. Zo krijgen we de uitslag van figuur 16.

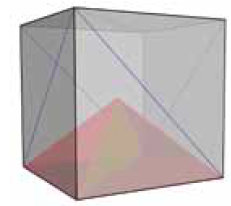
Figuur 15

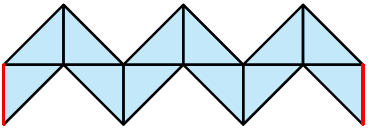
Figuur 16

Nu moeten de piramides nog op de halve vlakken worden geplaatst. Dus ook de piramides moeten we diagonaal door het grondvlak snijden. In figuur 15 zie je in rood hoe de piramide in de kubus is gepositioneerd en in geel de snede in de piramide. Nu hoeft er niets aan de snedes te worden gerekend, omdat de piramides precies door de topribben worden gesneden; deze ribben hebben we in het vorige nummer al bepaald. De vermoedelijke bedenker van deze constructie is Yoshimoto; hij heeft deze constructie in de vorm van een puzzel in 1988 op de markt gebracht.

Van kubussenoctaëder naar rombendodecaëder

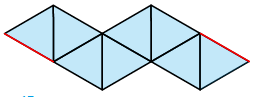
Figuur 17

In figuur 17 zie je een uitslag van de octaëder. Als de rode zijden aan elkaar worden bevestigd, krijgen we een band, maar de octaëder ontstaat nog niet automatisch zoals bij de uitslagen van de tetraëder en de kubus. Er moet wat worden gevouwd om de figuur te krijgen. Er is dus ruimte aanwezig, maar die is niet voldoende om de invariant om te kunnen keren. We zullen de vlakken daarom moeten snijden. Het is niet mogelijk, zoals bij de tetraëder, om alle vlakken doormidden te snijden en zo een aangesloten lint te krijgen. De sneden lopen dan van de top van de octaëder naar de hoek die op dezelfde hoofddiagonaal ligt. Dit is dus de onderste hoek. Zo ontstaan vier losse delen.

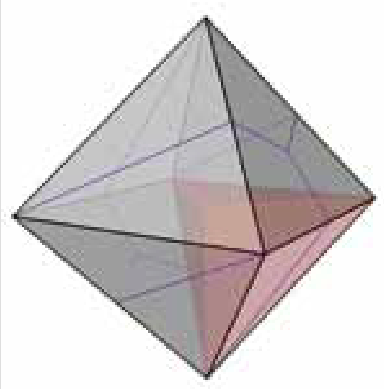
Figuur 18

Alle vlakken in drieën snijden gaat ook niet: dan krijgen we acht losse delen. Wel kunnen we twee tegenover elkaar gelegen vlakken in drieën snijden. De overige vlakken worden dan in tweeën gesneden (zie figuur 18). Met blauwe lijnen zijn de snedes weergegeven. In figuur 19 zie je de uitslag: deze is veel langer dan de gebruikelijke uitslag!

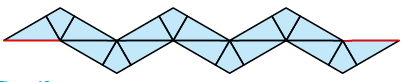
Figuur 19

Als we op de uitslag piramides willen plaatsen, zullen we zes piramides doormidden moeten snijden en twee in drie delen. In de vorige Pythagoras hebben we bij deze invariant aan beide zijden piramides geplaatst. Aan de ene kant van de invariant hadden de piramides de maximale hoogte en aan de andere kant werden piramides geplaatst die waren gebruikt bij de tetraëder. Deze piramides waren minder hoog en hiermee kon de rombendodecaëder worden gevormd.
Ook nu gaan we aan beiden zijden van de invariant dezelfde piramides plaatsen. In figuur 18 zie je in de octaëder een rode piramide die de maximale hoogte heeft. Aan de buitenzijde zie je eveneens een rode piramide, maar die is minder hoog (en afkomstig van de tetraëder). Van de kleinste piramides hebben we hierboven (‘van tetraëder naar triakistetraëder’) de snedelengtes (grondvlak en zijvlak) van de halve piramides al bepaald. Alleen de snedelengtes van de driedelige piramides moeten we nog bepalen. De snede van het zijvlak is even lang als bij de tweedelige piramide, omdat de lengte alleen wordt bepaald door het midden van de ribbe van het grondvlak en de top. De snedelengtes in het grondvlak bespreken we straks. Eerst kijken we naar de grotere piramides.

De snede van het grondvlak bij de halve piramides is bij de grote piramides even lang als bij de kleine piramides, want die wordt alleen bepaald door de grootte van de vlakken van de invariant. De snede van het zijvlak is anders, maar niet moeilijk te berekenen. De lengte van de topribben en het grondvlak weten we al van het vorige artikel. De topribben hebben lengte $\sqrt{2}$ en de ribben van het grondvlak hebben lengte 2 (zie figuur 20). Opnieuw kun je $s$ met Pythagoras berekenen. Het kan overigens ook door de helft van de ribbelengte van de octaëder te nemen.

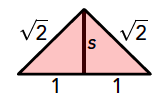
Figuur 20

Het enige dat nog moet worden bepaald, is de snedelengtes in het grondvlak als de grote en kleine piramide in drieën worden gesneden (zie figuur 5).
Bij driehoeken is bekend dat het zwaartepunt op een derde van de hoogte ligt. En omdat de driehoeken gelijkzijdig zijn, loopt de hoogtelijn van de top door het zwaartepunt naar het midden van de zijden. Daarom liggen de snedes op de hoogtelijn en hebben een lengte die een derde is van de hoogte.
Hiermee hebben we alle maten en afmetingen en kunnen we naar de bouwtekeningen van de drie constructies kijken. Veel plezier bij het construeren van de figuren!

Bouwtekeningen

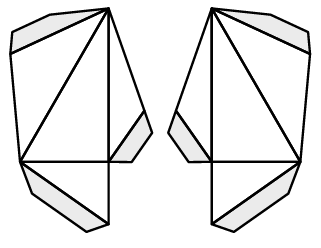
Figuur 21 Bouwtekening invariant tetraëder; 4 keer nodig

Figuur 21 is de bouwtekening van de tetraëder als invariant. Op de eerste foto van figuur 22 zie je hoe je de halve piramides aan elkaar moet bevestigen. Ter verduidelijking kan je de uitslag van figuur 11 erbij nemen. Op de tweede foto zie je de tetraëder en op de derde de triakistetraëder.

Figuur 22

Figuur 23 is de bouwtekening van de kubus als invariant. De eerste en tweede foto van figuur 24 (en de uitslag van figuur 16) laten zien hoe je de halve piramides onderling aan elkaar moet bevestigen. Zo kunnen de kubus (derde foto) en de rombendodecaëder (vierde foto) worden gemaakt.

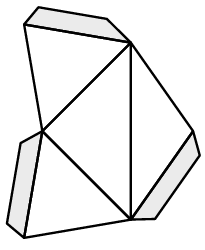
Figuur 23 Bouwtekening invariant
kubus; 12 keer nodig

Figuur 24

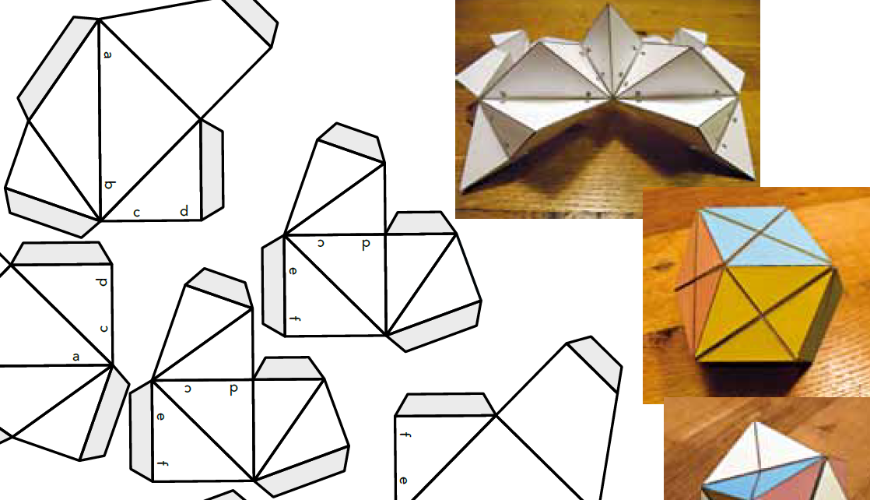
Figuur 25 is de bouwtekening van de octaëder als invariant. Omdat de invariant bij deze constructie geheel in de constructie valt en daardoor helemaal niet zichtbaar is, kun je niet goed gebruikmaken van de uitslag in figuur 19 als hulpmiddel bij het in elkaar zetten van de band. Daarom zijn op de bouwtekeningen letters aangebracht. Na het in elkaar lijmen van de delen, kun je de delen op de juiste manier aan elkaar bevestigen door overeenkomstige letters bij elkaar te zoeken, zie de eerste foto van figuur 26. Op de tweede foto zie je de rombendodecaëder en op de derde foto de kubussenoctaëder.

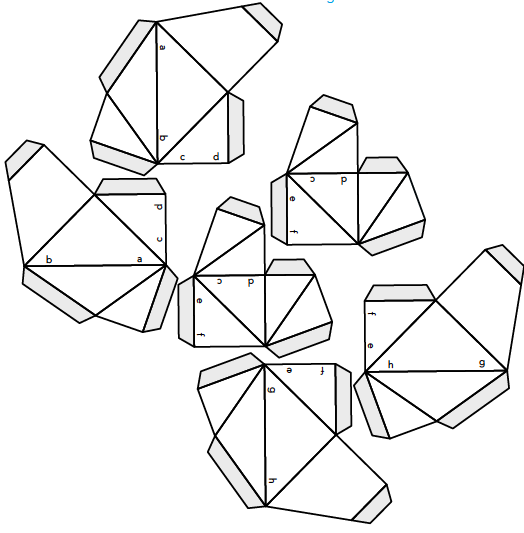
Figuur 25 Bouwtekening invariant octaëder; 3 keer nodig

Figuur 26