Het Spel NIM
In dit artikel analyseren we het bekende spel Nim. Kun je dit spel altijd winnen, als je maar slim genoeg bent? We starten met eenvoudigere spellen en geven een algemene methode voor een winnende strategie.
Kegelspel
Twee spelers spelen een spel met een rij rechtop staande kegels. De eerste speler moet één kegel of twee naburige kegels wegnemen. De overige kegels blijven op hun plek staan. Dan doet de tegenstander hetzelfde, enzovoort. Wie de laatste kegel(s) wegneemt, is de winnaar.

In figuur 1 zie je een voorbeeld van een spelverloop met acht kegels. Speler A neemt de kegels 5 en 6 weg. Dan is speler B aan zet: hij neemt de tweede kegel. Speler A neemt vervolgens kegel 7. Als B nu slim is, neemt hij de kegels 3 en 4. Daarna moet A wel 1 of 8 nemen, zodat B de laatste kegel krijgt en wint.
Kunnen we een systeem bedenken waarbij we vanaf het begin al weten wie er wint? Bij een rij van één of twee kegels wint de beginner. En bij een rij van drie neemt de beginner de middelste weg, waarna zijn tegenstander niet beide mag nemen en de beginner dus de derde en laatste kegel kan pakken. Maar hoe zit het vanaf vier kegels?
Opdracht 1. Laat zien dat de beginner altijd kan winnen, hoeveel kegels er ook in de startrij staan. Denk daarbij aan het begrip symmetrie. In figuur 2 hieronder zie je twee spellen, één met een even aantal kegels (tien) als startrij en één met een oneven aantal (zeven). De eerste zet is al door middel van een omcirkeling aangegeven. Hoe nu verder?

Welke spellen bekijken we?
We bestuderen spellen die gespeeld worden door twee spelers die om beurten een zet doen. Er is een beginstand en er wordt op de een of andere wijze vastgesteld wie de eerste zet doet. Na elke zet komt er een nieuwe en andere stand. Twee keer dezelfde stand mag niet voorkomen, anders zou het spel oneindig lang kunnen duren. We beschouwen alleen spellen die na een eindig aantal zetten eindigen. Dan wordt volgens een van tevoren vastgestelde winstregel vastgesteld wie de winnaar is.
elangrijk is ook, dat alle informatie over de loop van het spel bij iedereen bekend is. Het kaartspel bridge bijvoorbeeld voldoet daar niet aan: voor elke speler zijn de kaarten in de hand van de andere spelers onbekend.
Nog iets: voor beide spelers gelden precies dezelfde regels om een zet te doen. We noemen deze spellen onpartijdige spellen (Engels: impartial). Er zijn ook zogenaamde partijdige (Engels: partisan) spellen, waarin voor beide spelers verschillende regels gelden om te zetten. Schaken is zo’n spel: wit mag alleen met de witte stukken zetten en zwart alleen met de zwarte.
In dit artikel bekijken we dus eindige onpartijdige spellen met volledige informatie.
Kaarten wegnemen en omdraaien
We geven een voorbeeld: leg een aantal kaarten naast elkaar op tafel met allemaal het plaatje boven. Twee spelers, B (beginner) en T (tegenstander), moeten om beurten een kaart wegnemen en een andere kaart omdraaien. Het aantal kaarten in de rij neemt dus na elke zet met één af. Als er nog één kaart op tafel ligt, is het spel afgelopen. Als iemand erin slaagt met zijn laatste zet een kaart achter te laten met het plaatje boven, dan heeft hij gewonnen. Als degene die de laatste zet doet niet anders kan dan de laatste kaart achter te laten met de achterkant boven, heeft hij verloren.
Welke strategie moet de beginner B volgen om altijd te winnen? Of is het zo dat de tegenstander T altijd kan winnen? Of is het afhankelijk van het aantal kaarten waarmee ze beginnen?
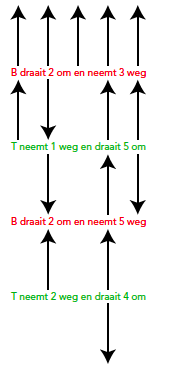
Opdracht 2. In figuur 3 zie je een spel, beginnend met vijf kaarten. Een pijltje naar boven betekent een kaart met het plaatje boven. Na vier zetten heeft de tegenstander een dichte kaart achtergelaten en dus verloren. Maar heeft hij wel de goede strategie gevolgd? Probeer eerst zelf de oplossing te vinden voor dit spel met vijf kaarten, voor je verder leest. Hoe zit het met grotere even of oneven startaantallen?
Nim
Een van de mooiste spellen in de groep van eindige impartiale spellen met volledige informatie is Nim, waarin aan het begin een aantal stapeltjes $(1, 2, 3, 4, 5, …)$ munten, lucifers of knopen op tafel liggen. De beginaantallen kunnen willekeurig gekozen worden. De regel om te zetten is: een speler neemt van een van de stapels één of meer munten weg. Die spelen verder geen rol meer. Het aantal munten neemt dus na iedere zet af en zal uiteindelijk nul worden.
De winstregel is: wie geen zet meer kan doen, verliest. Dus wie geconfronteerd wordt met de eindsituatie met nul munten op tafel, verliest.
Één stapel munten
Neem een stapel met een flink aantal munten. Als de gewone Nimregels gelden, wint natuurlijk de beginner, want hij neemt alle munten weg. Dit is een al te simpel spel. Als extra regel kunnen we bijvoorbeeld toevoegen: je moet minstens één en hoogstens drie munten pakken.
Als je tegenstander aan zet is met een stapel van vier, kan hij ze niet allemaal wegnemen. Hij moet er echter wel minstens één wegnemen. Dan neem jij de rest weg en win je. Misschien kun je met dit gegeven vinden welke standen met je tegenstander aan zet voor jou allemaal gewonnen zijn.
Twee stapels munten
Ook met twee stapels is Nim nog niet zo ingewikkeld. Als de beginner B twee stapels van ongelijke grootte voor zich heeft, zal hij altijd kunnen winnen. Noem de aantallen $p$ en $q$ en de stand $(p, q)$. Zodra een van de stapels nul munten bevat, neemt hij de tweede stapel geheel weg en wint, dus $(p, 0) \to (0, 0)$. Als er geen stapel leeg is, neemt hij van de grootste stapel er zoveel weg dat beide stapels gelijk zijn, dus met $p > q: (p, q) \to (q, q)$. Als de tegenstander T alles wegneemt van een stapel, neemt B de rest. Als T niet een gehele stapel wegneemt, maakt B de stapels weer gelijk. Net zo lang tot B de eindstand $(0, 0)$ bereikt en dus wint. Voor B zijn dus alle standen $(p, q)$ met $p \neq q$ winnend.
De loop van een spel
Laten we eens proberen de volledige loop van een onpartijdig en eindig spel grafisch weer te geven. Elke stand van het spel geven we weer met een punt. Bij een eindig spel zijn er dus eindig veel verschillende standen, die elk hun eigen punt hebben in de tekening. Teken nu een beginpunt, het punt behorend bij de beginstand. Vanuit deze stand kan de beginner B een aantal zetten doen, die tot verschillende nieuwe standen leiden. Dit geven we aan met verbindingslijnstukken. Deze verbindingslijnstukken tussen de punten kunnen we voorzien van een pijl om aan te geven dat de zet de ene stand naar een andere laat overgaan. Het schema van punten en lijnstukken heet een graaf en als de lijnstukken een richting hebben spreken we van een gerichte graaf.
Het kan best voorkomen dat een punt al bereikt is via een andere zettenroute. Omdat we te maken hebben met een eindig spel, zullen we echter nooit op een stand terechtkomen die we al gepasseerd hebben. Uiteindelijk zal een eindstand bereikt worden, waarna geen zet meer gedaan kan worden. Degene die dan weer moet zetten, heeft verloren.
Het hoeft niet zo te zijn dat er altijd geëindigd zal worden met dezelfde stand: dat hangt af van het winstcriterium. Als je bij voorbeeld in het bovenstaande Nimspel met twee stapels niet als winstcriterium neemt dat iemand de laatste munt wegneemt, maar dat je wint als je een enkele stapel met één munt achterlaat, zijn er twee eindsituaties denkbaar: $(0, 1)$ en $(1, 0)$.
ij beperken ons echter tot spellen die uiteindelijk leiden tot een enkele eindstand. Bij het Nimspel met twee stapels is dit $(0, 0)$ en bij een Nimspel met vijf stapels is het $(0, 0, 0, 0, 0)$.
Beste strategie bij (2, 2)-Nim
We kunnen het spel Nim weergeven in een gerichte graaf waarmee we het spel beter gaan begrijpen. In figuur 4 is de graaf weergegeven die hoort bij Nim met twee stapels van elk twee munten. We weten al dat dit spel verloren is voor de beginner. We laten dit nog eens zien aan de hand van figuur 4.
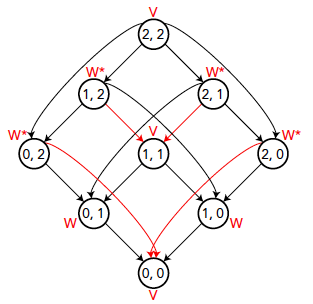
en 2. De rode pijlen geven de juiste keuze aan.
In de cirkeltjes staat telkens de stand: de aantallen van de twee stapeltjes. De codes W en V staan voor winnende en verliezende situaties en komen ons straks van pas. We gaan ervan uit dat het spel gespeeld wordt door twee ideale spelers: zij maken geen enkele fout. Het lijkt dan duidelijk dat óf de beginner altijd kan winnen, óf zijn tegenstander.
We starten met de eindsituatie $(0, 0)$ en werken vanuit het einde terug. De speler die in deze situatie moet zetten, kan geen zet meer doen en heeft verloren (V). Vervolgens gaan we één zet terug en zoeken alle standen die zeker overgaan in $(0, 0)$. Dat zijn alleen $(1, 0)$ en $(0, 1)$. (Weliswaar kun je van $(2, 0)$ en $(0, 2)$ ook naar $(0, 0)$ overgaan, maar dat is niet verplicht. Daarom bekijken we die punten nu nog niet.) De speler die in een van deze standen moet zetten, laat vervolgens dus zeker $(0, 0)$ achter en is dus de winnaar (W). We gaan weer een zet terug en zoeken alle standen die na één zet een van de drie al van een code voorziene standen opleveren. Dat zijn de standen (0, 2), (1, 1) en (2, 0). Weliswaar kun je vanuit de twee standen (1, 2) en (2, 1) ook een van deze drie standen bereiken, maar vanuit (1, 2) of (2, 1) leiden niet alle zetten naar een van deze drie standen. Deze twee standen bespreken we later.
Eerst bekijken we (1, 1). Van daaruit bereikt de speler (1, 0) of (0, 1), die beide code W hebben. De speler zal dus aan zijn tegenstander een winnende stand geven en dus altijd verliezen. Daarom staat er een V bij. Nu bekijken we de stand (0, 2). Van daaruit zijn er twee mogelijkheden: naar (0, 1) met een W en (0, 0) met een V. In deze situatie moet de speler die aan zet is dus een keuze maken. Als hij (0, 1) met W achterlaat, zal hij verliezen. Maar als hij (0, 0) met V achterlaat, zal hij winnen. Hij kiest dus voor de stand met een V. We zetten bij (0, 2) de code W*. De ster betekent dat de speler hier de juiste keuze moet maken om een winnende strategie te vervolgen. We geven de juiste keuze aan door deze pijl rood te maken. Net zo komt er bij (2, 0) een W*.
We gaan nog een zet terug en zoeken alle standen die na één zet eindigen in een van de zes standen die al een code hebben: dat zijn (1, 2) en (2, 1). Niet (2, 2), want die kan overgaan naar (1, 2) of (2, 1), die nog geen code hebben.
We bekijken eerst (1, 2). Overgang naar (0, 2) of (1, 0) leidt naar een W, en zal dus verliezend zijn. Alleen overgang naar (1, 1) met een V leidt naar een verliezende stand voor de tegenstander. Die zet moet de speler dus doen om te winnen. Bij (1, 2) zetten we dus een W*. De ster staat er weer om aan te geven dat de juiste zet gedaan moet worden. We geven ook weer de juiste keuze aan in rood. Met dezelfde argumenten kunnen we bij (2, 1) een W* zetten.
Dan is er ten slotte alleen nog maar de beginstand (2, 2) nog niet voorzien van een code. Alle vier mogelijke zetten leiden naar een stand met code W. Wat de beginnende speler ook zet, hij zal altijd verliezen. De code is dus V. Conclusie: dit spel wordt verloren door de beginner.
Opdracht 3. Maak zelf een graaf voor een spel dat begint bij (2, 3), waarbij je steeds één of twee munten van een stapel mag nemen. Analyseer op bovenstaande manier of de beginner wint of verliest.
Opdracht 4. Maak zelf een graaf voor een spel dat begint met één stapel van acht munten, waarbij de spelers steeds één, twee of drie munten van de stapel mogen nemen. Analyseer op bovenstaande manier of de beginner wint of verliest. Kan je voorspellen wat er gebeurt als je met honderd munten start?
Algemene strategie
Tot zover de analyse van een simpel spel. Voor complexe spellen gaat de analyse voor een winnende strategie op dezelfde manier, alleen kan de bijbehorende graaf erg ingewikkeld worden. Begin met de eindstand en schrijf daar een V bij.
Zoek vervolgens alle standen die hier naartoe gaan. Deze krijgen een W. Vervolgens gaan we een zet terug en kijken we welke keuzes de speler maken. Er zijn steeds drie mogelijkheden voor de speler aan zet:
- Stel je voor dat de speler alleen kan zetten naar standen met een W. Dan zal hij met elke zet gaan verliezen en komt er een V bij de stand te staan.
- Stel je voor dat de speler alleen kan zetten naar standen met een V. Dan zal hij met elke zet gaan winnen en komt er een W bij de stand te staan.
- Stel je voor dat de speler naar allerlei standen kan, waar ook een V bij zit. Dan kiest hij natuurlijk voor een stand met een V. Er komt een W* bij deze toestand en een pijl naar de verliezende toestand met de V.
Uiteindelijk zal er bij de beginstand een W, een W* of een V komen te staan. In het eerste geval kan de beginner een winnende strategie volgen en in het tweede geval zal de beginner dus verliezen.
Om de winnende strategie te bepalen, zal je op deze manier de hele graaf moeten tekenen en voorzien van codes. Dat is in de meeste gevallen ondoenlijk, ook voor een computer. Voor een moeilijker spel zullen we dus alternatieven moeten zoeken. We weten inmiddels echter wel dat bij de spellen die we beschouwen en bij intelligent spel van beide spelers de beginner óf altijd kan winnen, óf altijd zal verliezen.
Drie stapels munten
Nim wordt pas echt moeilijk als we drie stapels munten nemen. De spelregels blijven gelijk: we mogen steeds één of meer munten wegnemen van één stapel. We geven een stand aan met $(p, q, r)$, waarbij we steeds de stapels munten rangschikken naar grootte. De eindstand is dan (0, 0, 0) met natuurlijk code V. Laten we eens proberen de eenvoudigste standen te beschouwen.
Van de standen $(0, p, p)$ weten we dat de beginner verliest en van de standen $(0, p, q)$ met $p \neq q$ weten we dat de beginner wint. In het bijzonder is ook de stand (0, 1, 1) verliezend. Een stand met twee enen en een ander getal is winnend. Immers, $(1, 1, p)$ gaat over in (0, 1, 1) en die stand is verliezend.
De eenvoudigste stand met drie aantallen ongelijk aan 0 die voor degene aan zet verloren is, is (1, 2, 3). Immers, als je bij deze stand een heel stapeltje wegneemt, houd je (1, 2, 0), (1, 0, 3) of (0, 2, 3) over. Deze zijn allemaal winnend, volgens de strategie hierboven. Als je niet een heel stapeltje wegneemt, houd je altijd twee gelijken over, namelijk (1, 1, 3) of (1, 2, 2). Als jij dan de afwijkende verwijdert, heb je (0, 1, 1) of (0, 2, 2). Deze zijn allebei verliezend.
Als je aan zet bent, dan is de volledige rij verliesgevende drietallen $(1, p, q)$ met $1 < p \leq q$ gegeven door
$$(1, 2, 3), (1, 4, 5), (1, 6, 7), (1, 8, 9), (1, 10, 11), (1, 12, 13), (1, 14, 15), … $$
Dit is als volgt in te zien. Elk drietal $(1, p, q)$ met $1 < p \leq q$ dat niet in deze rij voorkomt, is in een enkele zet in een van de standen van deze rij over te voeren. Bijvoorbeeld (1, 5, 9) kan in één stap worden gebracht naar (1, 4, 5).
Omgekeerd brengt elke zet, startend in een drietal in deze rij, je buiten deze rij. Óf je zit boven het drietal (1, 2, 3), óf je zit er onder:
- Als je onder (1, 2, 3) uitkomt, betreft dit een van de winnende drietallen (1, 2, 2), (1, 1, 2), (0, 1, 2), (1, 1, 3), (0, 1, 3) of (0, 2, 3).
- Als je in een drietal uitkomt boven (1, 2, 3), ben je in één stap weer terug in deze rij. Daarna ga je weer buiten de rij en er weer in, enzovoort, net zolang totdat je onder de (1, 2, 3) komt. Daar kom je alleen maar op een winnende stand.
De bovenstaande verliesgevende rij heeft de eigenschap dat in elke volgende stand de twee grootste aantallen telkens met 2 opgehoogd zijn. Na enig zoeken vinden we de rij standen verloren voor degene aan zet met als kleinste aantal 2:
$$(2, 4, 6), (2, 5, 7), (2, 8, 10), (2, 9, 11), (2, 12, 14), (2, 13, 15), (2, 16, 18), (2, 17, 19), …$$
Je ziet dat nu viertallen opeenvolgende getallen een rol spelen: 4, 5, 6, 7 in de eerste twee standen, 8, 9, 10, 11 in de volgende twee, 12, 13, 14, 15 in de volgende twee enzovoort.
Bij de verloren standen met als kleinste aantal 3:
$$(3, 4, 7), (3, 5, 6), (3, 8, 11), (3, 9, 10), (3, 12, 15), (3, 13, 14), (3, 16, 19), (3, 17, 18), …$$
allen weer de viertallen 4, 5, 6, 7 en 8, 9, 10, 11 en volgende op.
De verloren standen met 4 als kleinste aantal zijn: $$(4, 8, 12), (4, 9, 13), (4, 10, 14), (4, 11, 15), (4, 16, 20), (4, 17, 21), (4, 18, 22), (4, 19, 23), …$$ Het vinden van al deze drietallen vergt wel wat werk, maar al snel vind je de systematiek zelf. Je ziet in de laatste reeks de achttallen 8, 9, 10, 11, 12, 13, 14, 15 en 16, 17, 18, 19, 20, 21, 22, 23 verschijnen.
ls je nu een aantal van deze standen uit je hoofd leert (het hoeven er niet zoveel te zijn), en je slaagt erin een van deze standen te maken met je zet, dan zal jouw tegenstander die dan aan zet is, gaan verliezen, want je kunt telkens je tegenstander opschepen met een kleinere verliezende stand.
Machten van twee
Op de een of andere manier lijken de getallen 2, 4, 8 – de machten van 2 dus – een rol te spelen bij het analyseren van de standen die tot winst leiden. De eerste die heeft gedacht aan de mogelijkheid om de aantallen munten in elke stapel in het tweetallig stelsel (zie het kader op de volgende pagina) te schrijven, is vermoedelijk Charles Bouton, in 1901.
We bespreken deze speciale strategie aan de hand van een voorbeeld. Neem als beginstand (9, 12, 14). We zullen straks zien dat we alle andere beginstanden op dezelfde wijze kunnen onderzoeken.
Schrijf de drie aantallen in het tweetallig stelsel en zet ze onder elkaar (zie figuur 5 links). Tel deze getallen op een bijzondere manier op. Als er een even aantal enen onder elkaar staat, komt in de ‘som’ 0, en als er een oneven aantal enen onder elkaar staat, komt er in de ‘som’ 1. Dan is de som van de drie tweetallig geschreven aantallen munten ‘1011’.
De 0 geeft dus alleen maar aan dat er een even aantal gelijke machten van 2 in de 3 aantallen van de stapels zijn, en een 1 dat er een oneven aantal machten van 2 zijn. Als er één of meer enen in de som zijn (hier het eerste, derde en vierde cijfer), dan noemen we de ‘som’ oneven. Als er alleen nullen staan, noemen we de ‘som’ even.
Wat gebeurt er als een speler een even stand voor zich heeft en moet zetten? Hij maakt dus van een van de drie aantallen een ander getal. Dan zal dus op minstens een van de plaatsen in dit tweetallig geschreven getal een 1 in een 0 veranderen of een 0 in een 1. Als er namelijk niets verandert, neemt hij ook niets weg. Maar dan komt er op die plaats een 1 in plaats van een 0 in de ‘som’, en is de ‘som’ dus oneven.
Nu is het zo dat als degene aan zet een oneven ‘som’ voor zich heeft (dus in dit geval, want er staan drie enen in de ‘som’), hij een winnende strategie heeft. Deze strategie om te winnen, die we dadelijk ook zullen bewijzen, is nu de volgende.
Maak in de volgende zet de ‘som’ even. Als het altijd mogelijk zou zijn om van een willekeurige oneven stand een even stand te maken, dan zal de tegenstander weer een oneven stand moeten maken (net boven aangetoond) en de beginner weer een even stand kunnen maken, net zolang tot alle stapels leeg zijn en de beginner weer ‘0000’ achterlaat, waarna de tegenstander niet meer kan zetten en verloren heeft.
Het bewijs
In figuur 5 (links) met stand ‘1011’ kijk je naar de meest linkse 1 in de ‘som’. Die komt er door de ‘som’ van drie enen. Dan nemen we die 1 in gedachten. Het kan ook zijn dat het eerste cijfer in de ‘som’ een 0 is en pas het tweede een 1. Dan nemen we dat cijfer 1 in gedachten. In ieder geval vinden we een ‘eerste’ 1 van links, omdat de ‘som’ oneven is. In ons geval hebben we de som van drie enen. We mogen nu kiezen van welke stapel we een aantal munten afnemen om de ‘som’ ‘0000’ te maken. Er zijn drie winnende zetten. Hebben we maar een enkele 1, dat hebben we maar één winnende zet. In ons geval is elke 1 goed. Kies de stapel van 1410 om er een aantal munten vanaf te nemen. Neem er in ieder geval voorlopig 8 af, dat wil zeggen dat de eerste 1 een 0 wordt en het eerste cijfer in de ‘som’ dus 0. Dat gaat al goed. Het tweede cijfer is al een 0, dus daar hoeven we ons niet om te bekommeren. Het derde cijfer is weer een 1. Dus we zullen er nog 2 moeten wegnemen om dit cijfer in de ‘som’ ook 0 te maken. In totaal hebben we er nu al $8 + 2 = 10$ weggenomen. Maar we zijn er nog niet. Het vierde cijfer in de ‘som’ is ook een 1, maar in het tweetallige 14 staat op plaats 4 een 0. Nu moeten we er dus een munt bijdoen om deze 0 tot 1 te verhogen. Als we nu dus in totaal van de stapel van 14 er $8 + 2 – 1 = 9$ wegnemen, waarbij de speler er dus 5 laat liggen, krijgen we voor de aantallen van de drie stapels de getallen rechts in figuur 5.
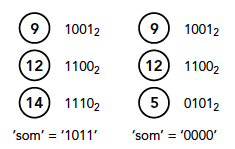
Door slechts een aantal munten van één enkele stapel weg te nemen, is de speler erin geslaagd er een even stand van te maken. De tegenstander zal dan weer een oneven stand maken, enzovoort, tot de speler alle stapels 0 kan maken en winnend eindigt.
Er is nog wel een puntje dat aandacht verdient. Om het laatste cijfer in de ‘som’ 0 te maken, moesten we er weer een munt bij doen. Dat zou natuurlijk op alle plaatsen kunnen gebeuren na de 1 die als eerste is weggenomen. Stel je voor dat dit zo zou zijn, dan neem je er 8 voorlopig weg en moet je er nog $4 + 2 + 1$ bij plaatsen om de overige cijfers in de ‘som’ 0 te maken. En $1 + 2 + 4 = 7 < 8$. Dus dat kan altijd. Je neemt er dan in ieder geval de verplichte 1 weg. Bij grotere aantallen lukt dat natuurlijk ook. Bijvoorbeeld: $1 + 2 + 4 + 8 + 16 =2^0 + 2^1 + 2^2 + 2^3 + 2^4 = 31 < 32 = 2^5$.
Als je deze speelwijze hanteert, moet je eigenlijk een papiertje hebben om de aantallen tweetallig te schrijven. Maar als je een beetje handig bent, kun je de munten bijna ongemerkt in machten van twee ordenen, terwijl je ze schijnbaar aan het tellen bent. Dan zie je snel welke machten van twee een even aantal of een oneven aantal keer voorkomen. Zo kun je dus met deze strategie vrijwel altijd winnen. Alleen als je tegenstander de tweetallige strategie ook kent, en in een oneven stand aan zet is, zal hij jou dus steeds een even ‘som’ ‘0000’ geven en dus gaan winnen.
Getallen in het tweetallig stelsel
In het door ons gebruikte tientallig stelsel om getallen te noteren, schrijven we elk getal als de som van een aantal machten van $10: 10^0 = 1, 10^1 = 10, 10^2 = 100, 10^3 = 1000$ enzovoort. Zo betekent het getal $4273_{10}$ het volgende: $4 × 10^3 + $2 × 10^2+7 × 10^1 + 3 × 10^0$. De index 10 achter het getal 4273 geeft aan dat we te maken hebben met een getal in het tientallig stelsel.Op dezelfde wijze kunnen we een getal in het tweetallig stelsel schrijven, door het te schrijven als de som van een aantal machten van 2. Als voorbeeld geven we het tientallige 85: $$85_{10}$ = 1 × 2^6 + 0 × 2^5 + 1 × 2^4 + 0 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 1010101_2,$$ met de index 2 om aan te geven dat we een getal in het tweetallig stelsel bedoelen.
Grotere en meerdere stapels munten
Bij grotere stapels munten krijgen we natuurlijk tweetallig geschreven aantallen van meer dan 4 cijfers en ook sommen van meer dan 4 cijfers. Maar dat doet aan de winststrategie natuurlijk niets af. Van een even stand met ‘som’ ‘000…00’ moet je altijd een oneven stand maken, en van een oneven stand kun je altijd een even stand maken.
De tweede uitbreiding is er door niet 3, maar 4, 5, 6 of meer stapels munten te nemen. Maar ook dan schrijven we natuurlijk elk aantal weer in het tweetallig stelsel, zetten de aantallen onder elkaar en tellen ze op onze bijzondere manier op. Dan hebben we weer even standen met ‘000…00’ of oneven standen met minstens een 1 erin. De methode om van een oneven stand met een aantal enen de stand met ‘som’ ‘000…00’ te maken, is dan ook weer dezelfde.
Nu hebben we alle Nimspellen waarbij je als zet één of meer munten van een willekeurige stapel weg moet nemen, geanalyseerd. Degene die aan zet is en een even stand met ‘som’ ‘000…00’ kan afleveren, zal winnen