Je bent ongetwijfeld gewend aan het tekenen van grafieken in een tweedimensionaal assenstelsel. Op de horizontale as zetten we doorgaans de variabele $x$ en op de verticale as de $y$.
Vaak wordt het verband tussen $x$ en $y$ gegeven door een speciale formule. Met de variabele $x$ voeren we een berekening uit en de uitkomst geven we weer met de $y$. Zo’n verband heet een functie: $y = f(x)$. De punten $(x, y)$ vormen de grafiek van de functie $f$. Eigenschappen van de formule kan je terugvinden in de grafiek en je kan proberen bij grafieken met speciale eigenschappen een goede formule te vinden.
Zo weten we dat $y = 2x – 1$ de grafiek van een rechte lijn is en we weten ook dat hij de $y$-as snijdt in –1. Omgekeerd weten we dat een (niet-verticale) rechte lijn voor te stellen is door de formule $y = ax + b$, waarbij je $a$ en $b$ nog wel moet berekenen.
Voor parabolen kan je net zoiets doen: we weten dat $y = x^2 – 4x$ als grafiek een parabool heeft. Allerlei eigenschappen zijn weer uit de formule af te leiden. Omgekeerd kan je elke dal- en bergparabool, dus elke parabool die symmetrisch is ten opzichte van een verticale lijn, schrijven als $y = ax^2 + bx + c$ met $a$ ongelijk 0.
Je kan het steeds ingewikkelder maken en het is leuk om de formules van zo mooi mogelijke grafieken te verzinnen.

Verder dan een functie

Als je de formule van een cirkel wilt geven, dan kan dat niet meer met een functie. Functies hebben namelijk de eigenschap dat voor elke $x$-waarde hoogstens één ywaarde getekend kan worden. Om leuke figuren te maken is de functie dus beperkt. De formule van de cirkel met als middelpunt de oorsprong en straal 1 is
$$x^2 + y^2 = 1.$$
Als je deze cirkel wilt tekenen, neem je bijvoorbeeld een vaste waarde voor $x$ en je rekent $y$ uit. Je krijgt dan $y = \sqrt{(1 – x^2)}$ en $y = –\sqrt{(1 – x^2)}$. Dit zijn dus eigenlijk twee functies.

Hoe zou je moeilijkere formules kunnen tekenen? Neem als voorbeeld de vergelijking
$$x^3 – y^3 + 3xy = 0.$$
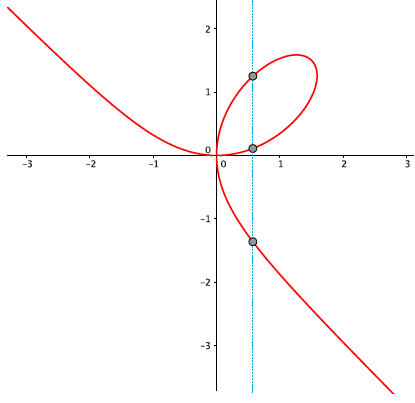
Voor elke $x$ kan je deze vergelijking oplossen: je krijgt steeds een derdegraadsvergelijking in $y$. Deze heeft één, twee of drie oplossingen. In figuur 1 is een $x$ aangegeven waarvoor er drie verschillende waarden $y$ bestaan die voldoen aan de vergelijking. Deze prachtige figuur heet het folium van Descartes.
Aan dit voorbeeld kan je zien dat met wat ingewikkelder formules heel interessante figuren te maken zijn. Je kan het zelf met GeoGebra proberen

Drie dimensies

Als je een dimensie toevoegt, de $z$-as, wordt alles een stuk ingewikkelder. We hebben wel dezelfde opbouw als boven. We kunnen een formule met $x$ en $y$ maken en de uitkomst als $z$ noteren. We krijgen zo een variabele $z$ die afhangt van $x$ en $y$, ofwel de functie $z = f(x, y).$

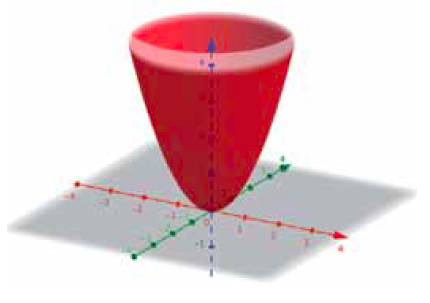
De functie $$z = 2x + y + 1$$ is een vlak dat de $z$-as snijdt in 1. De formule lijkt sterk op het tweedimensionale geval $y = f(x)$. Je kan je dit vlak voorstellen als je voor y steeds andere waarden invult: er staat dan steeds de vergelijking $z = 2x + c$ met $c$ het getal $y + 1$. Moeilijkere functies geven interessantere figuren. De formule $$z = x^2 + y^2$$ koppelt aan elk punt $(x, y)$ in het platte vlak een waarde $z$. Ook zo’n formule is nog wel te begrijpen: als we de waarde van $z$ constant houden (niet negatief), dan staat er precies de vergelijking van een cirkel met straal $\sqrt{z}$. Als je $y = 0$ neemt, staat er de parabool $z = x^2$. Ook dit kan je prima proberen met GeoGebra (zie figuur 2).

Het wordt echt ingewikkeld, maar ook spannend, als we een vergelijking in drie variabelen proberen te tekenen. Een eenvoudig voorbeeld is $$x^2 + y^2 + z^2 − 1 = 0.$$ Deze levert een bol op met straal 1. Als je een coëfficiënt verandert en bijvoorbeeld $$x^2 + y^2 + 3z^2 − 1 = 0$$ tekent, blijk je meer een soort M&M te krijgen. Je kunt het nog veel moeilijker maken dan bovenstaande voorbeelden. Van vergelijkingen als
$$x^2y^2 + y^2z^2 + z^2x^2 – xyz = 0$$
kan je je niet zomaar voorstellen hoe ze eruit zullen zien. Omdat je de $x$, $y$ en $z$ kan verwisselen zonder dat de vergelijking verandert, zal het object er wel van allerlei kanten hetzelfde uit moeten zien. Op zo’n manier komen er soms heel mooie vormen tevoorschijn.

De tentoonstelling

We hebben gezien dat het meestal niet eenvoudig is om je een driedimensionaal object voor te stellen als je alleen de vergelijking kent. Vroeger maakte men dan soms mooie gipsen modellen van zo’n oppervlak. Maar tegenwoordig is er natuurlijk software waar je het veel makkelijker mee kunt laten zien.
Op de reizende tentoonstelling Imaginary, die dit schooljaar op verschillende plekken in het land te zien is, kun je dergelijke visualisaties zien die gemaakt zijn met het softwarepakket SURFER. Er hangen posters waarop iets verteld wordt over de vergelijking. Ook kun je ter plekke zelf dingen proberen in SURFER. Daarnaast kun je nog een aantal oude gipsmodellen zien, naast moderne 3D-geprinte modellen van dezelfde objecten.
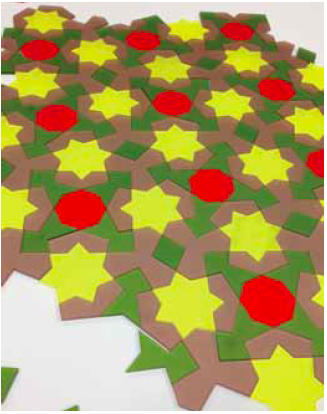
De focus van de tentoonstelling ligt op het visueel maken van de wiskunde. De platen zien er allemaal mooi uit. Bij visuele wiskunde horen uiteraard ook de beroemde tweedimensionale vlakvullingen (zie figuur 3). Voor mensen die het leuk vinden om gewoon met mozaïeken aan de slag te gaan, staat er dan ook een tafel met mooi afgewerkte mozaïekstukjes waar je beroemde patronen mee kunt maken, bijvoorbeeld de Penrosebetegelingen of Islamitische mozaïeken.

Om plezier te hebben met Imaginary hoef je er niet eens per se naar toe. De website http://www.imaginarymaths.nl geeft al een heleboel informatie, posters en filmpjes. Daar zijn ook voorbereidingswerkbladen te vinden voor docenten die er met een klas naar toe gaan, maar nog veel leuker: je kunt via de site ook de SURFER-software downloaden en er zelf mee gaan tekenen! Imaginary was tot begin november te zien in Enschede en doet vanaf 21 november achtereenvolgens de volgende steden aan: Amsterdam, Utrecht, Leiden, Groningen en Nijmegen. Een impressie van de tentoonstelling en meer informatie, onder andere over de openingstijden en reserveringen voor schoolklassen, vind je op http://www.imaginarymaths.nl. 

Wedstrijd voor mooiste object

De Duitse Valentina Galata, nu promovendus bio-informatica, ontdekte de SURFER-software toen ze in 2008 als scholier bij een Imaginarytentoonstelling kwam en raakte erdoor gefascineerd. Ze slaagde erin talloze combinaties van vergelijkingen te maken die beschrijvingen zijn voor alledaagse objecten als een theepot, fruit, landschappen, schaakstukken, noem maar op. In navolging daarvan is er nu een prijsvraag gekoppeld aan de tentoonstelling: wie maakt het mooiste object in SURFER? Je kunt meedoen tot 31 juli 2017.