De vergelijking van een cirkel

De vergelijking van een cirkel met straal $r$ en middelpunt $(a, b)$ wordt gegeven door
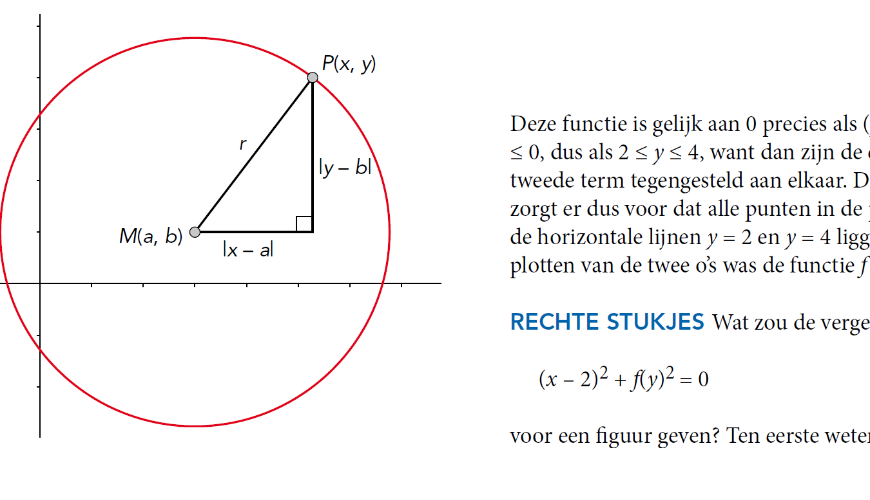
$$(x – a)^2 + (y – b)^2 = r^2.$$Je kunt dit begrijpen met de stelling van Pythagoras: de afstand tussen het middelpunt $M(a, b)$ van de cirkel en een punt $P(x, y)$ op de cirkel is gelijk aan $r$ (zie figuur 2). In de rechthoekige driehoek zijn de lengtes van de rechthoekzijden $|x – a|$ en $|y – b|$, en is $r$ de lengte van de schuine zijde. De formule van een cirkel met middelpunt $M(3, 3)$ en straal 1 is dus $(x – 3)^2 + (y – 3)^2 = 1$.
Dit kan je een klein beetje anders schrijven: $(x – 3)^2 + (y – 3)^2 – 1 = 0.$ Net zo is de cirkel met middelpunt $M(6, 3)$ en straal 1 gegeven door $(x – 6)^2 + (y – 3)^2 – 1 = 0$. We kunnen deze twee cirkels in één formule samenvatten: $$((x – 3)^2 + (y – 3)^2 – 1) · ((x – 6)^2 + (y – 3)^2 – 1) = 0.$$
Als de coördinaten van een punt aan deze vergelijking voldoen, is een van de twee factoren van de vergelijking gelijk aan 0. Het punt ligt dus op een van beide cirkels. De tekening die bij deze vergelijking hoort, geeft dus deze twee cirkels. Merk op dat er niks verandert als we het linkerlid kwadrateren.
 

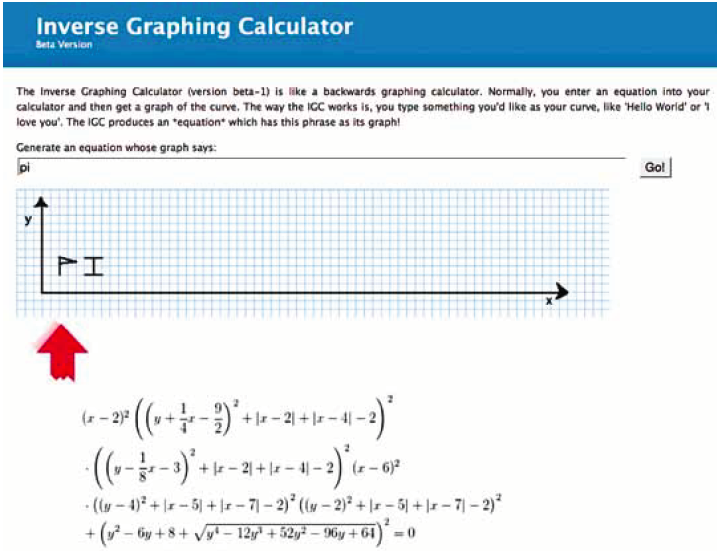
Figuur 1 Een schermafbeelding van de inverse graphing calculator met invoer ‘pi’

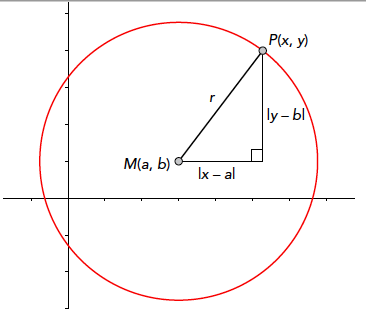
Figuur 2 De afstand tussen het middelpunt $M(a, b)$ van een cirkel met
straal r en een punt $P(x, y)$ op de cirkel is gelijk aan $r$

Inverse graphing calculator

Als je op de betreffende website het woord ‘oo’ invoerde, gaf het programma als uitvoer:
\begin{align*}&((x – 3)^2 + (y – 3)^2 – 1)^2 \cdot \\ &((x – 6)^2 + (y – 3)^2 – 1)^2 + f(y)^2 = 0,\end{align*}
waarbij $$f(y) = y^2 – 6y + 8 + \sqrt{y^4 - 12y^3 + 52y^2 - 96y+64}.$$
De eerste term van de vergelijking herkennen we. Waar is die tweede term $f(y)^2$ voor nodig?

Uiteraard is $f(y)^2$ groter dan of gelijk aan 0, want het is een kwadraat. Hetzelfde geldt voor de eerste term in de vergelijking. Dit betekent dat als $f(y)$ ongelijk aan 0 is, de eerste term negatief moet zijn. Dit kan niet vanwege de kwadraten. Net zo: als de eerste term ongelijk aan 0 is, moet $f(y)^2$ kleiner dan 0 zijn en dit kan ook niet. We besluiten: als de coördinaten $(x, y)$ van een punt voldoen aan deze vergelijking, dan zullen beide termen gelijk zijn aan 0.
We zullen nu de tweede term analyseren.

Eenvoudiger

Het programma schrijft $f(y)$ op een nogal moeilijke manier. Er geldt namelijk:
$$y^4 – 12y^3 + 52y^2 – 96y + 64 = (y – 4)^2 (y – 2)^2$$ en
$$y^2 – 6y + 8 = (y – 4)(y – 2). $$
Hieruit volgt dat $$f(y) = (y – 4)(y – 2) + |(y – 4)(y – 2)|.$$
Deze functie is gelijk aan 0 precies als $(y – 4)(y – 2) \leq 0$, dus als $2 \leq y \leq 4$, want dan zijn de eerste en de tweede term tegengesteld aan elkaar. Deze functie zorgt er dus voor dat alle punten in de plot tussen de horizontale lijnen $y = 2$ en $y = 4$ liggen! Voor het plotten van de twee o’s was de functie f niet nodig.

Rechte stukjes

Wat zou de vergelijking
$$(x – 2)^2 + f(y)^2 = 0$$
voor een figuur geven? Ten eerste weten we dat $2 \leq y \leq 4$, vanwege $f(y) = 0$. Ten tweede moet tegelijkertijd gelden dat $(x – 2)^2 = 0$, dus $x = 2$. Deze vergelijking stelt dus een verticaal lijnstuk tussen de punten (2, 2) en (2, 4) voor.
En wat geeft de vergelijking
$$(y – 2)^2 + (|x – 2| + |x – 4| – 2) = 0?$$
We merken op dat $|x – 2| + |x – 4| – 2$ gelijk is aan 0 als $2 \leq x \leq 4$ en dat $|x – 2| + |x – 4| – 2$ positief is voor elke andere $x$. (Zie je waarom?) Conclusie: er zijn alleen punten die aan de vergelijking voldoen als $2 \leq x \leq 4$ en in dat geval is $y = 2$: een horizontaal lijnstuk dat de punten (2, 2) en (4, 2) verbindt.
Dit combinerend met de eerste vergelijking geeft
$$(x – 2)^2 · ((y – 2)^2 + (|x – 2| + |x – 4| – 2))^2 + f(y)^2 = 0,$$
een mooie formule voor de letter L. Als je ‘L’ invoert op de website, krijg je inderdaad precies deze formule.
Schuine lijnstukken zijn nu ook niet moeilijk meer. Welk lijnstuk wordt door
$$(y – \frac{1}{2} x – 2)^2 + (|x – 2| + |x – 4| – 2) = 0$$ voorgesteld? (Ter controle: voer ‘K’ in op de site.)

Tot slot

We zagen in de uitvoer steeds formules van het volgende type:
\begin{align*} A^2 + D^2 = 0 & \text{     of} & A^2 · B^2 + D^2 = 0,\end{align*}
of ingewikkelder. We kwamen erachter dat de termen gescheiden door een + allemaal tegelijkertijd 0 moeten zijn en dat bij de uitdrukkingen die met elkaar worden vermenigvuldigd er tenminste één nul moet zijn. We kunnen hier de optelling dus als het logische woord en beschouwen en de vermenigvuldiging als of.
Kan jij nu zelf andere vormen of lettertypes bedenken met algebraïsche formules?