OPGAVE UIT DE NEDERLANDSE WISKUNDE OLYMPIADE, EERSTE RONDE 2016

Zeven personen worden verdacht van diefstal:

• een bruinharige man met blauwe ogen;
• Boris, een blonde man met groene ogen;
• Chris, een blonde man met bruine ogen;
• Denise, een blonde vrouw met bruine ogen;
• Eva, een bruinharige vrouw met blauwe ogen;
• Felix, een bruinharige man met bruine ogen;
• Gaby, een blonde vrouw met blauwe ogen;

Detectives Helga, Ingrid en Julius weten dat n van de verdachten de dief is. Na wat speurwerk te hebben gedaan, delen ze de volgende informatie in een dialoog.

Helga: Ik weet de oog- en haarkleur van de dief, maar ik weet niet wie het is.

Ingrid heeft Helga niet gehoord en zegt: Ik weet de haarkleur en het geslacht van de dief, maar ik weet niet wie het is.

Julius ten slotte zegt: Eerst wist ik alleen het geslacht, maar na jullie uitspraken weet ik wie de dief is.

De detectives spreken de waarheid. Wie is de dief?

Om de opgave hiervoor op te lossen en uiteindelijk de dader te vinden, bekijken we de uitspraken van de drie detectives een voor een.

HELGA'S UITSPRAAK

Als eerste bekijken we de uitspraak van detective Helga. Zij zegt de oog- en haarkleur van de dief te weten, maar niet genoeg informatie te hebben om de identiteit van de dief te achterhalen. We maken een tabel met alle zeven verdachten, gesorteerd op hun oog- en haarkleur:

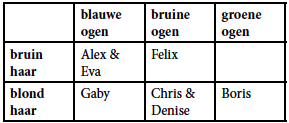
Wat kunnen we nu uit Helgas uitspraak afleiden? Stel dat de oog- en haarkleur van de dief allebei bruin waren. Dan had Helga, die al deze gegevens ook heeft, kunnen afleiden dat Felix de dief geweest zou zijn. Helga heeft de identiteit van de dief echter niet kunnen afleiden. Hieruit concluderen we dat de oog- en haarkleur van de dief niet allebei bruin zijn en dat Felix dus niet de dief is.

Op dezelfde manier kan Boris niet de dief zijn. Als Helga immers had geweten dat de dief blond haar en groene ogen heeft, dan had ze ook wel kunnen bedenken dat Boris de dief is en Helga weet juist niet wie de dief is. Ook kan Gaby geïdentificeerd worden aan de hand van haar oog- en haarkleur en zij kan dus ook niet de dief zijn.

Alex en Eva hebben echter allebei bruin haar en blauwe ogen. Dus ook al zou Helga geweten hebben dat de dief bruin haar en blauwe ogen heeft, dan nog wist ze niet wie van Alex of Eva de dief is. Chris en Denise hebben ook dezelfde kleur haar en ogen. Deze vier verdachten kunnen nog niet uitgesloten worden.

INGRIDS UITSPRAAK

Nu bekijken we de uitspraak van Ingrid. Ingrid heeft niet gehoord wat Helga zei en kan de informatie die hierboven is afgeleid uit Helgas uitspraak niet gebruiken. We beginnen dus weer met alle zeven verdachten. Ingrid weet de haarkleur en het geslacht van de dief, maar kan hiermee niet de identiteit van de dief bepalen. We maken weer een tabel:

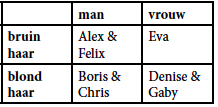
We gaan weer op dezelfde manier te werk. Als Ingrid had geweten dat de dief een bruinharige vrouw was geweest, dan had ze ook kunnen afleiden dat Eva de dief is. Ingrid weet de identiteit van de dief echter niet. De dief is dus geen bruinharige vrouw en is dus niet Eva.

In alle andere gevallen zijn er twee mogelijke dieven. Er zijn twee bruinharige mannen, Alex en Felix, twee blonde mannen, Boris en Chris, en twee blonde vrouwen, Denise en Gaby. Uit Ingrids uitspraak kunnen we dus alleen afleiden dat Eva niet de dief is, maar de andere zes kunnen niet door haar uitspraak uitgesloten worden.

JULIUS' UITSPRAAK

Nu gaan we de balans opmaken. Uit Helga's uitspraak hebben we afgeleid dat Boris, Felix en Gaby niet de dief zijn. Uit Ingrids uitspraak hebben we afgeleid dat Eva niet de dief is. De enige drie verdachten die nog overblijven zijn dus Alex, Chris en Denise.

Julius heeft de uitspraken van Helga en Ingrid wel gehoord en heeft dit ook kunnen afleiden. Dit is essentieel om tot de oplossing van het probleem te komen. Julius weet alleen het geslacht van de dief en zegt nu te kunnen afleiden wie de dief is. We maken een lijstje met de overgebleven verdachten:

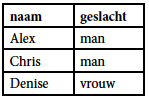
In Julius' lijstje staan twee mannen en een vrouw. Als Julius nu had geweten dat de dief een man is, dan had hij nog steeds niet kunnen weten of het nou Alex of Chris is. Julius kan echter wél uit de gegevens afleiden wie de dief is. Dan blijft er nog maar een optie over: de dief is een vrouw en ze heet Denise.

OPGAVE UIT DE JUNIOR WISKUNDE OLYMPIADE 2014

Er is een stuk appeltaart gestolen en vijf kinderen worden hierover ondervraagd. Ze weten allemaal wie het gedaan heeft, maar ze spreken niet allemaal de waarheid. Als een kind liegt, dan voelt het volgende kind zich daar zo schuldig over dat het juist de waarheid spreekt. De kinderen doen de volgende uitspraken in deze volgorde:

Asim: ‘Coen en ik hebben het allebei niet gedaan.’

Bob: ‘De dader is Coen of Dilan.’

Coen: ‘Eva en ik hebben het allebei niet gedaan.’

Dilan: ‘De dader is Asim.’

Eva: ‘Minstens twee van Asim, Bob, Coen en Dilan hebben gelogen.’

Wie heeft de appeltaart gestolen?

APPELTAART

We gaan naar de vraag over het stuk appeltaart, zie het kader rechts. Om dit probleem op te lossen, gaan we redeneren vanuit het antwoord. Voor elk van de mogelijke dieven bekijken we welke van de uitspraken er wel of niet waar zouden zijn. Asims uitspraak is waar als Bob, Dilan of Eva de dief is, en onwaar als Asim of Coen de dief is. We kunnen hetzelfde doen voor de uitspraken van Bob, Coen, Dilan en als laatste Eva en de resultaten in een tabel zetten:

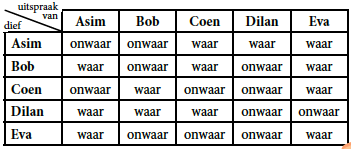
Nu gaan we door de lijst van dieven. Stel dat Asim de dief is. Dan bekijken we de rij van Asim in de tabel en zien we dat zowel Asim als Bob gelogen hebben. In de probleemstelling staat echter dat er nooit twee kinderen na elkaar liegen. Asim is dus niet de dief.

In de rij van Coen zien we dat Coen en Dilan na elkaar gelogen hebben, in de rij van Dilan zien we dat Dilan en Eva na elkaar gelogen hebben en in de rij van Eva zien we dat Bob en Coen na elkaar gelogen hebben. We zien dus dat Coen, Dilan en Eva ook niet de dief kunnen zijn.

De enige kandidaat die overblijft is Bob. We zien dat er in Bobs rij niet twee kinderen na elkaar liegen. Bob moet dus wel de dief zijn.

TOT SLOT

Het is ons gelukt: we hebben twee dieven gevonden! Door systematisch te werk te gaan en alle informatie in overzichtelijke tabellen te zetten, konden we in beide opgaven de dief vinden. Lijkt het je leuk om meer van dit soort problemen op te lossen? Neem dan eens een kijkje op de site van de Nederlandse Wiskunde Olympiade om oude opgaven te bekijken: http://www.wiskundeolympiade.nl. Of lees het boek Wanneer is Cheryl jarig? van Birgit van Dalen en Quintijn Puite; dat staat vol met logicapuzzels en andere leuke raadsels.